Graphing Linear Equations
Slope-Intercept Form
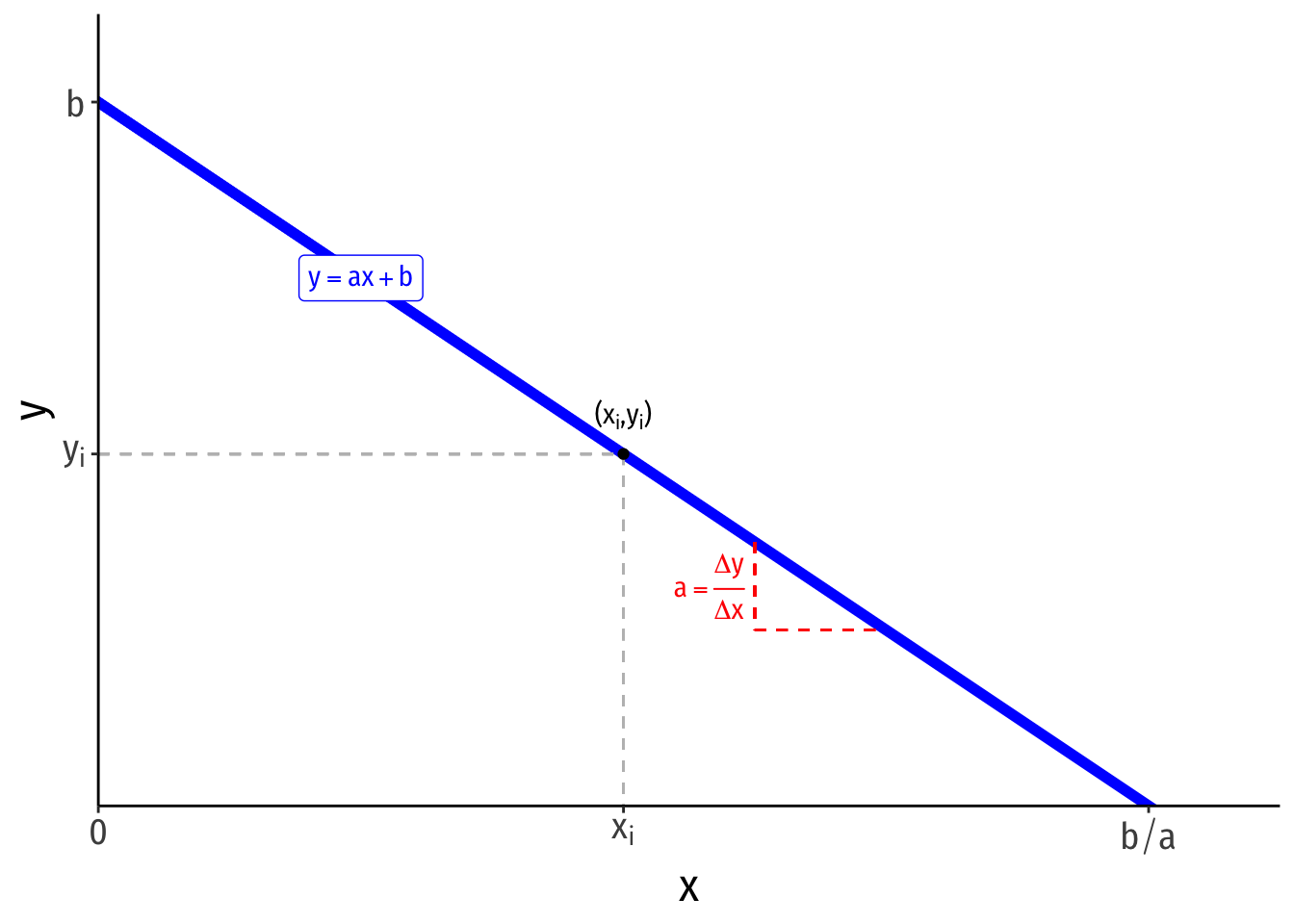
- A linear function of two variables can be written in slope-intercept form:
- you may have been taught the slope as “
- if
- if
- Any point on the line has an
Other Forms
- A linear function can equivalently be expressed in the following form:
This is a valid equation, but is difficult to visualize in the traditional graph as above. Simply solve for the dependent variable on the vertical axis
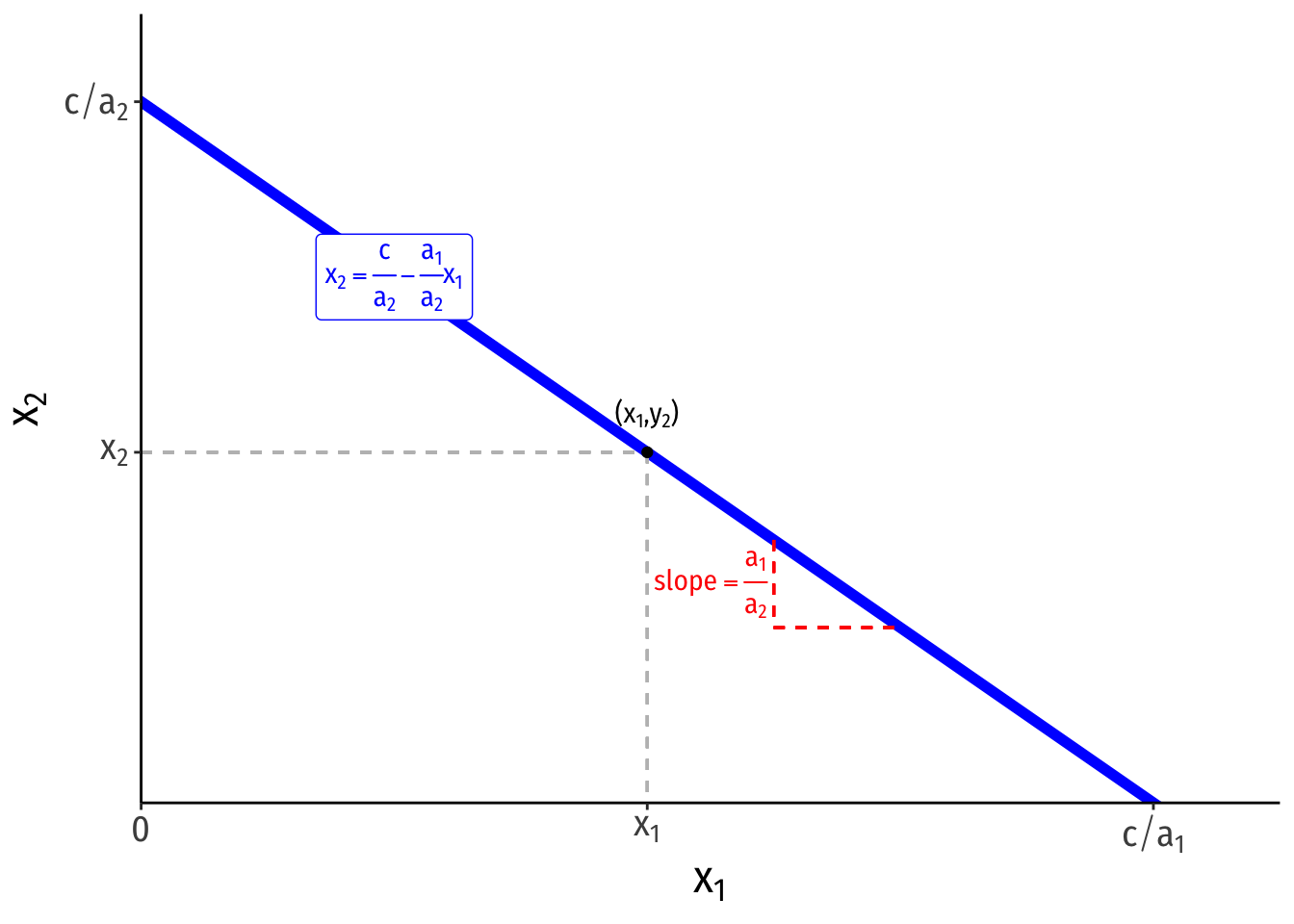
The vertical intercept is
The horizontal intercept is
The slope is
This is extremely useful for dealing with constraints in constrained optimization problems: budget constraints and isocost lines
Drawing a Graph From an Equation
If we already have a linear equation that we would like to graph, we can follow these steps:
- Take the equation and plug in two values, e.g. if we have:
- We can find two points on the graph. The easiest one to find is the vertical-intercept, where the line crosses the vertical axis, where
Thus, one point is
- For our second point, let’s plug in
Thus, another point is
- Now, plot the two points on the graph, and connect them with a line
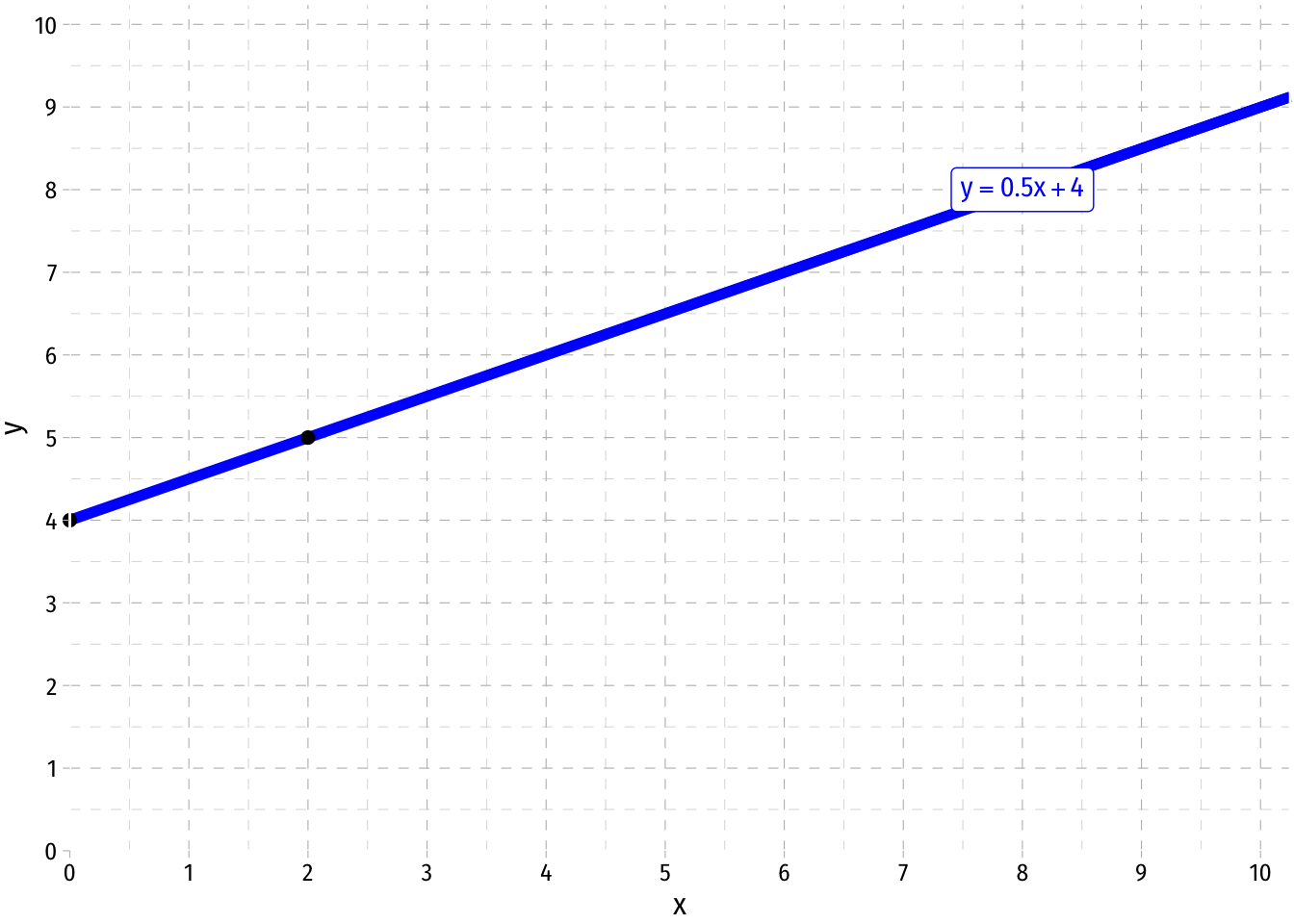
Note: A quick shortcut to plot a line is to find the vertical intercept and plot that, and then find the next point using the slope. Here, start our line at 4 on the vertical axis, and then, as the slope is
Finding an Equation from a Graph
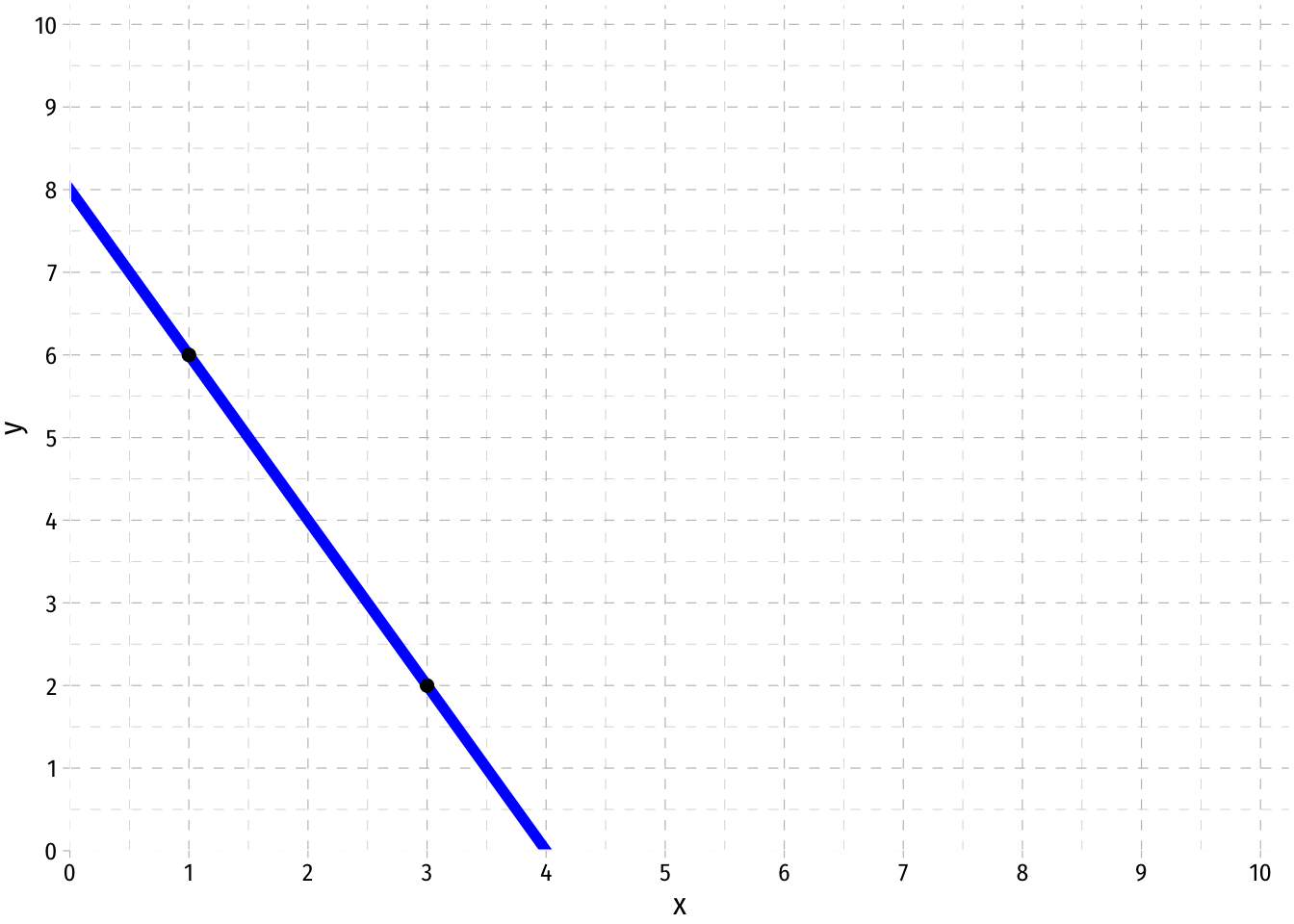
In order to find the equation of an existing line, we follow these steps:
- First, take two points on the line and find the slope,
There is a shortcut that we can use to find the slope faster by eye-balling the graph: When
- Now with the slope, we need to find the vertical intercept, or
Note, there is another easy way to eye-ball what this value is. It is simply that
- Thus, we have the slope and the intercept, so our equation is: