2.4 — Costs of Production — Appendix
From Total Product to Total Cost: Output Expansion Paths
We can trace the output expansion path (OEP) of a firm as the set of optimal (cost-minimizing combinations of inputs at constant prices) production points for different levels of output. These will be all of the tangencies for a given isoquant (output level) with the lowest possible isocost line.
Importantly, we are assuming: (1) firms always minimize total cost at every level of output; and (2) input prices
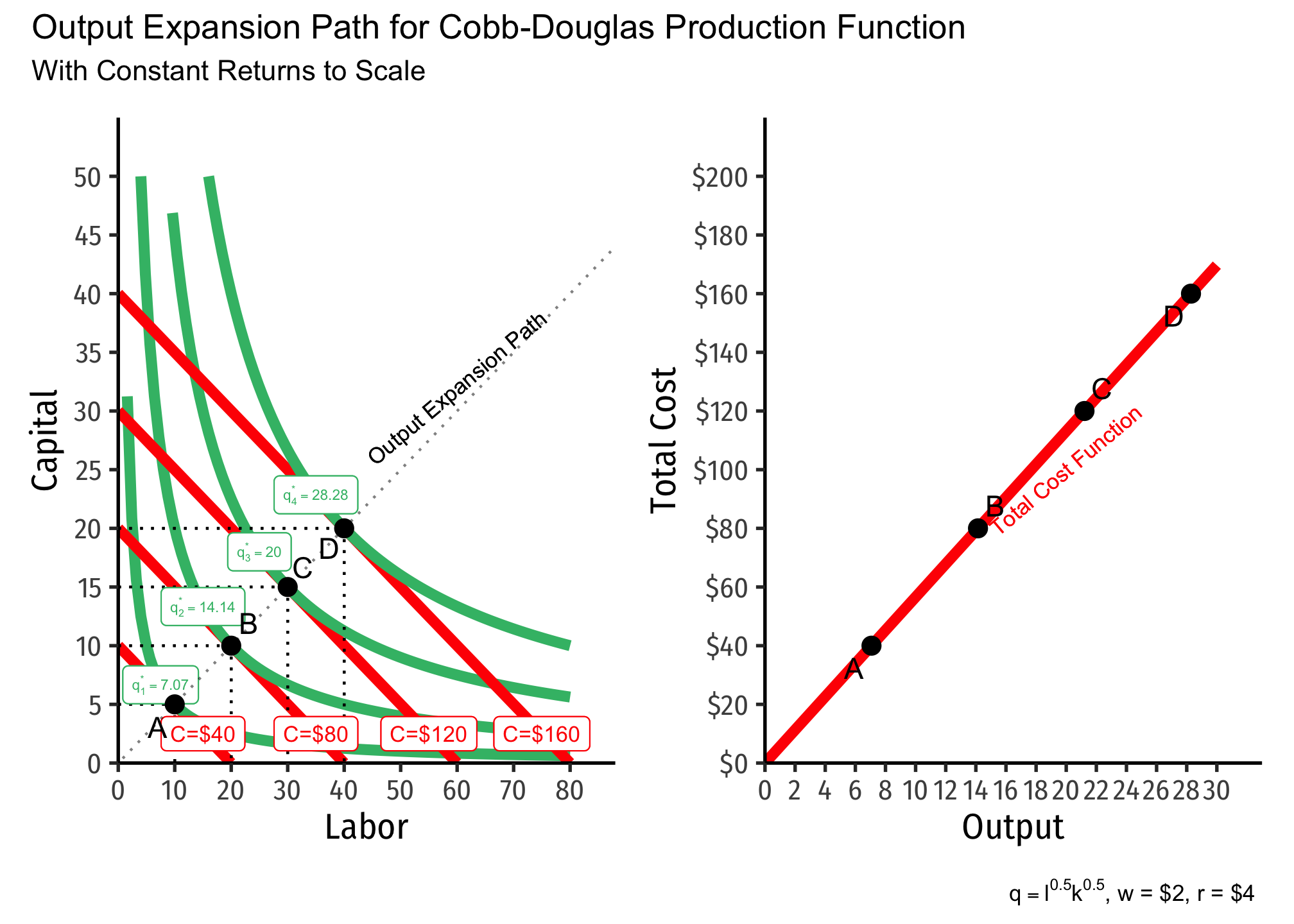
For a Cobb-Douglas production function, the OEP is a ray from the origin (0,0) through all the optimal combinations. Other production functions may have OEPs that are not straight lines, but curves.
We can trace the total cost function
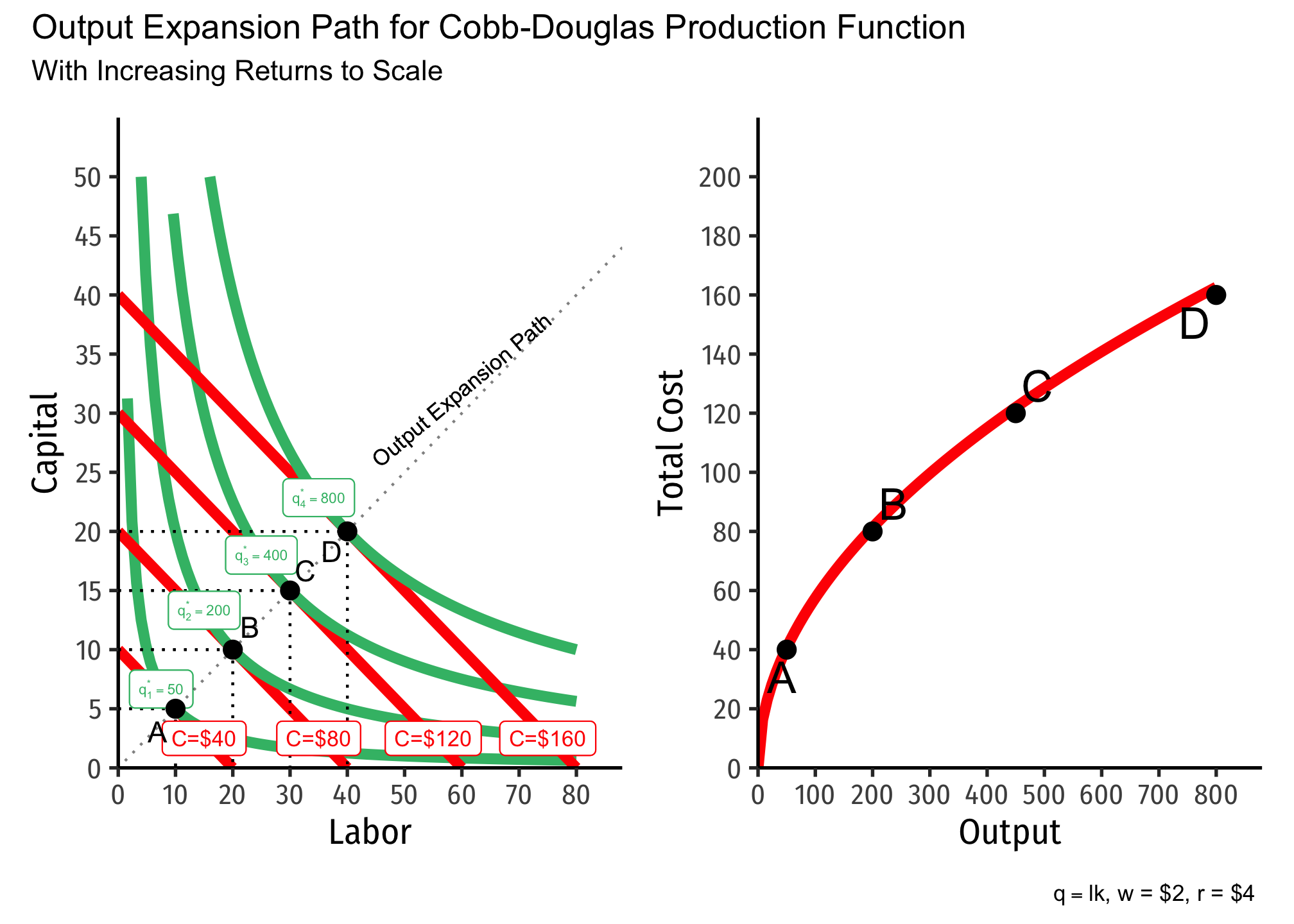
Note here we can also visualize the differences in returns to scale, and begin to see their connection to economies of scale (how output relates to average cost).
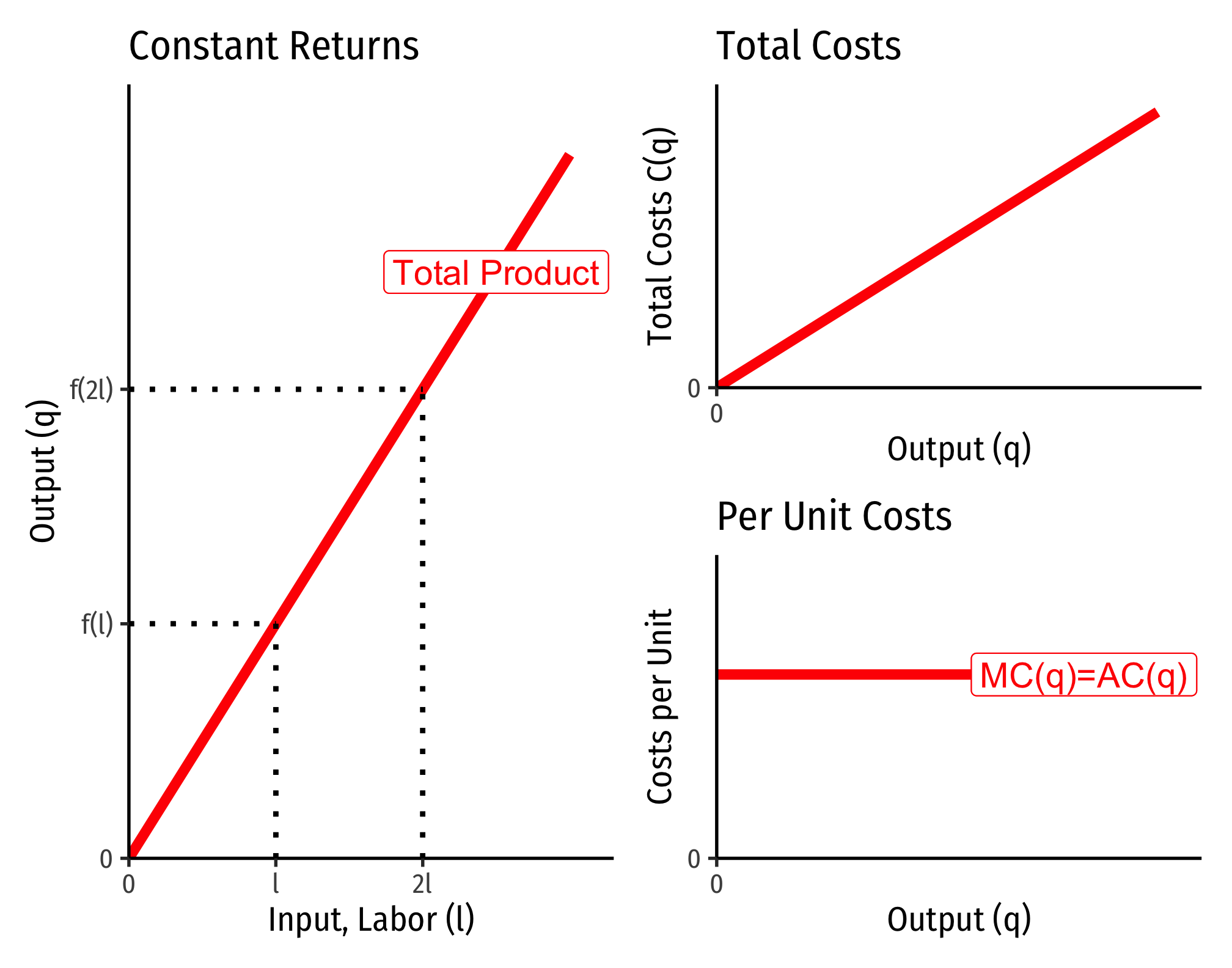
Below, I show the output expansion paths and total cost functions for technology with constant returns. Note that as we double the amount of inputs from point
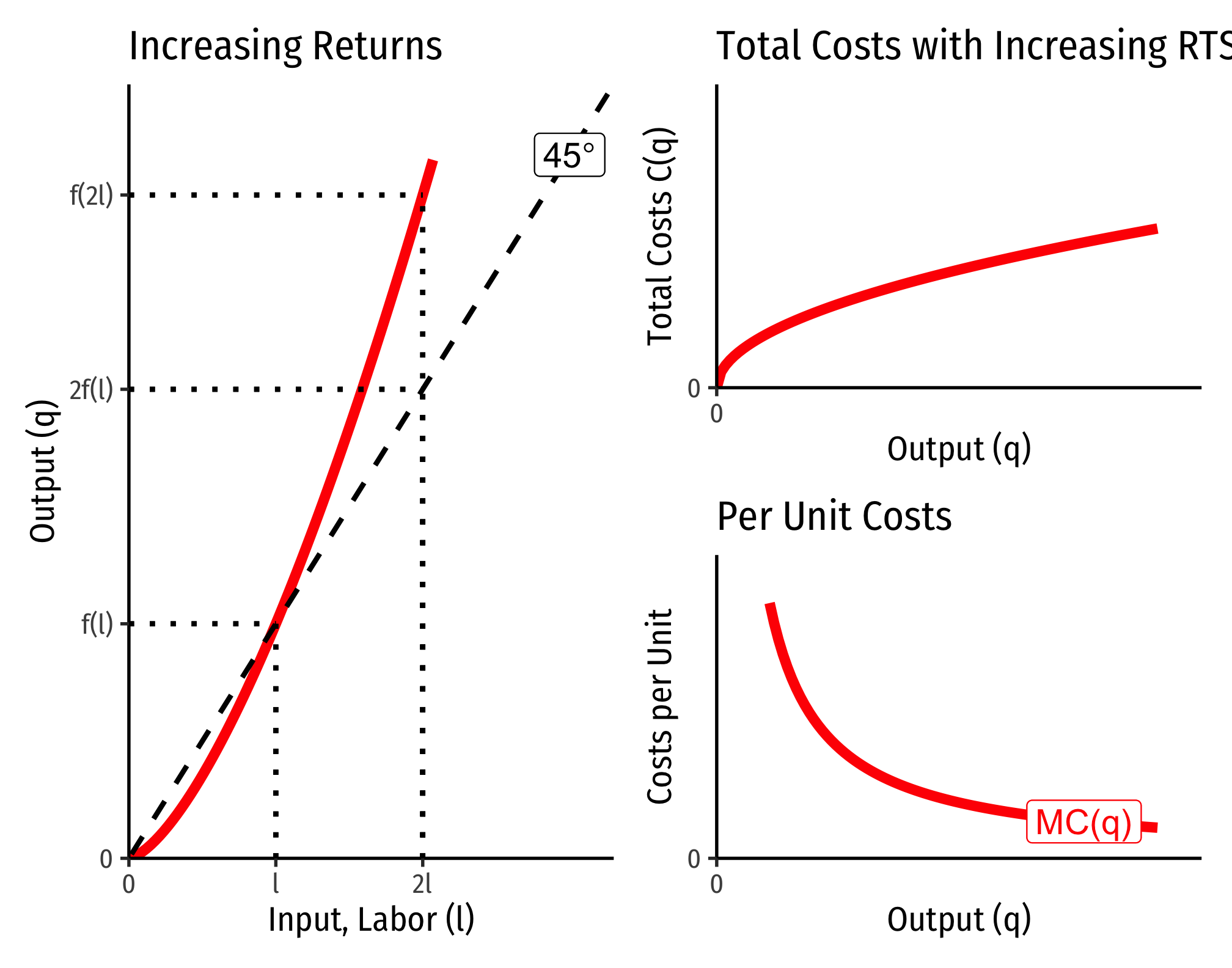
Below, I show the output expansion paths and total cost functions for technology with increasing returns. Note that as we double the amount of inputs from point
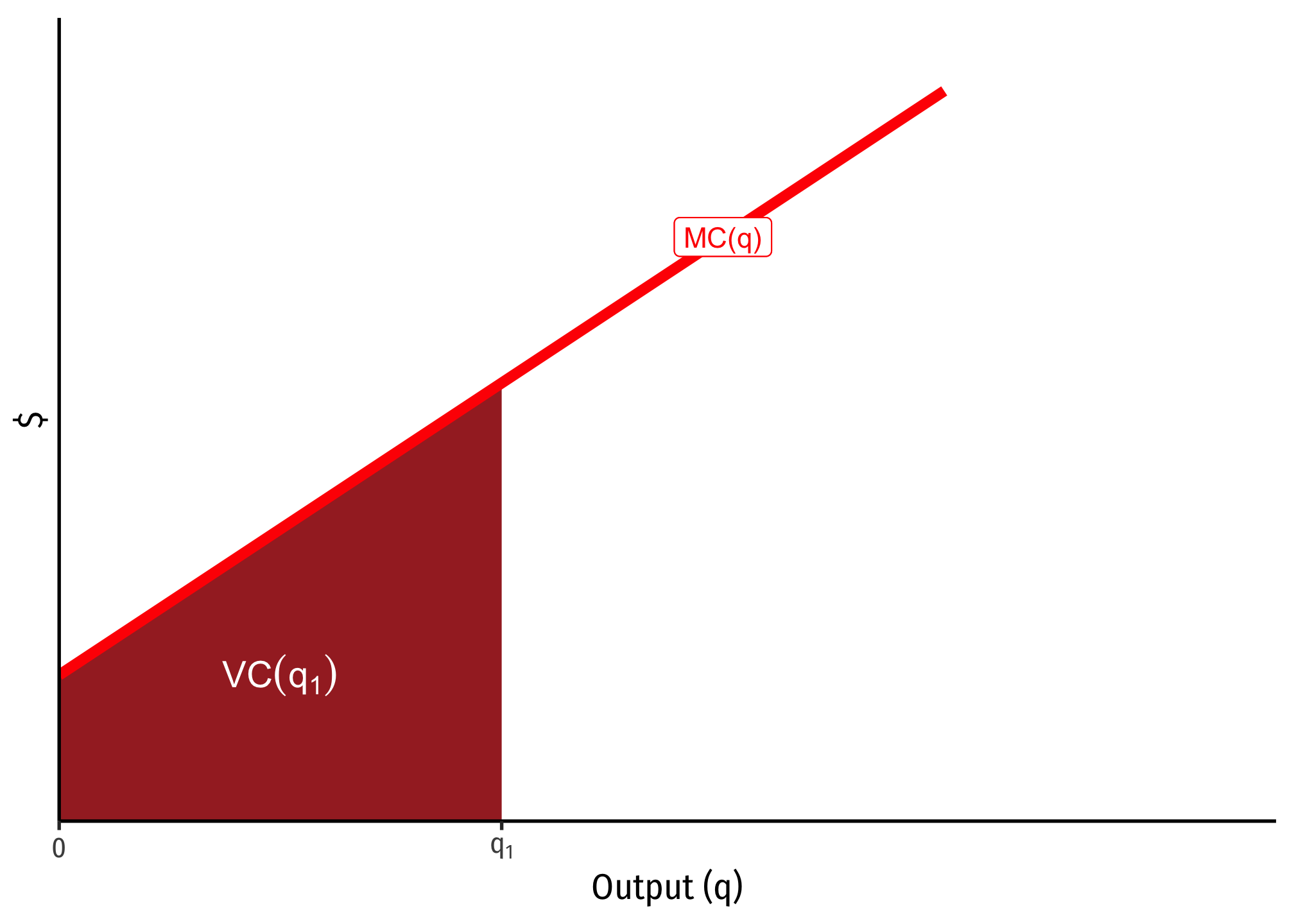
Marginal Cost and Variable Cost
Marginal cost is defined as the change in total costs from a change in output:
Recall that total cost is the sum of fixed and variable costs
However, since fixed costs never change, any change in total cost is a change in variable cost
Thus, marginal cost actually measures the change in variable costs from a change in output:
Thus, fixed cost has no effect on marginal cost, and marginal cost is always measuring the change in variable costs with additional output.
Furthermore, because of this relationship with marginal cost measuring the change in variable cost from additional output, for any specific quantity of output, e.g.
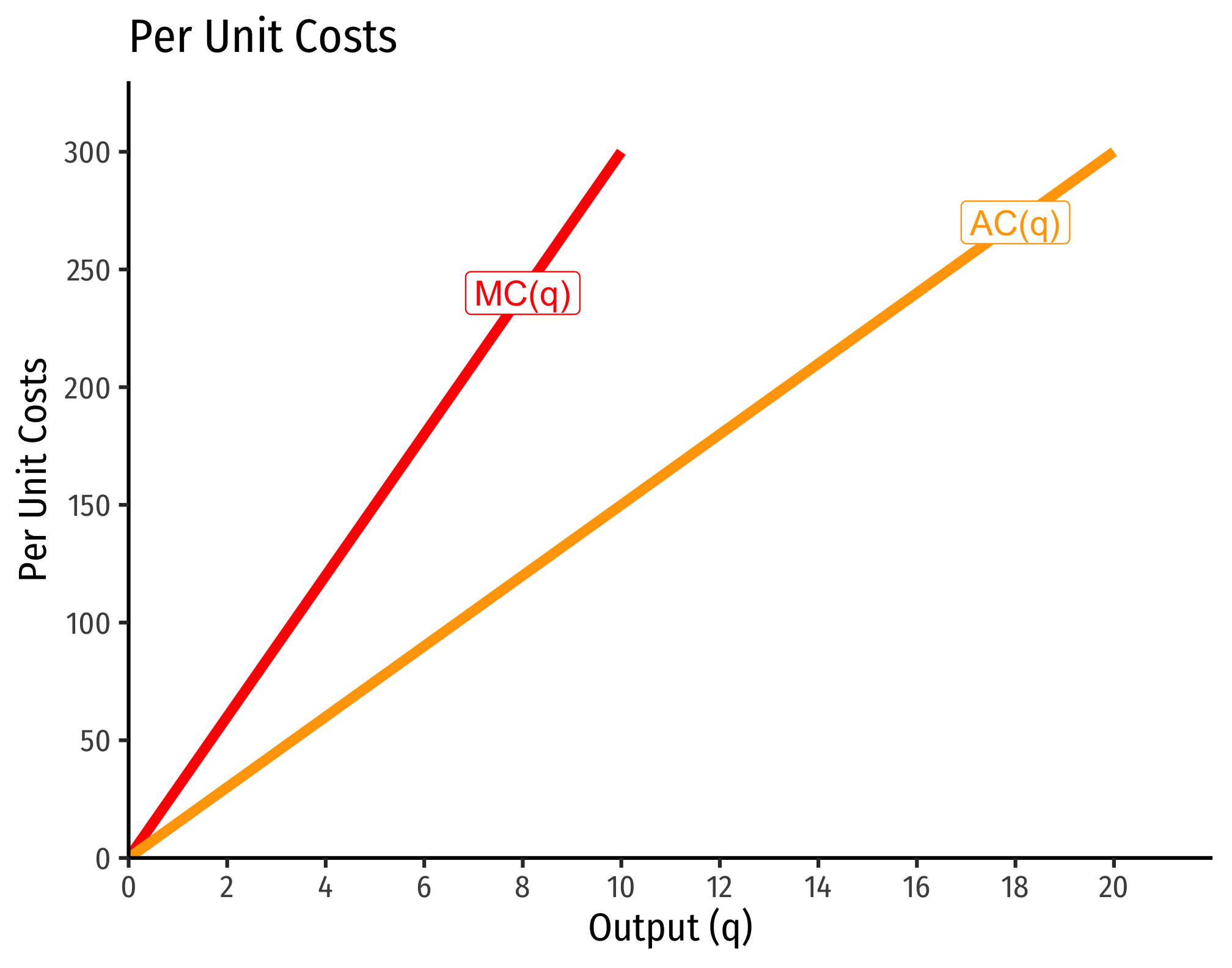
The Relationship Between Returns to Scale and Costs
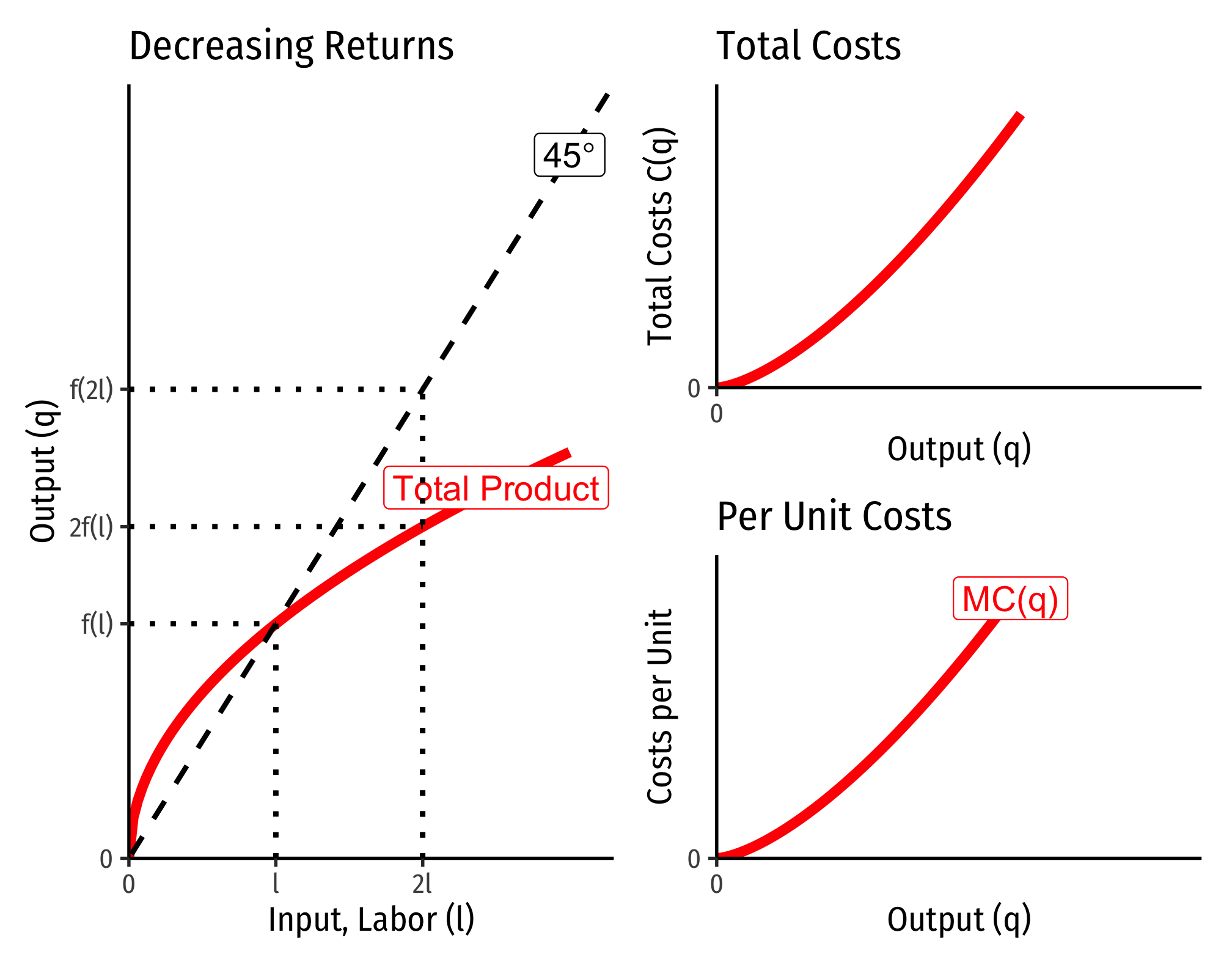
There is a direct relationship between a technology’s returns to scale1 and its cost structure: the rate at which its total costs increase2 and its marginal costs change3. This is easiest to see for a single input, such as our assumptions of the short run (where firms can change
Constant Returns to Scale:
Decreasing Returns to Scale
Increasing Returns to Scale
Cobb-Douglas Cost Functions
The total cost function for Cobb-Douglas production functions of the form
can be shown with some very tedious algebra to be:
If you take the first derivative of this (to get marginal cost), it is:
How does marginal cost change with increased output? Take the second derivative:
Three possible cases:
- If
- Production function exponents
- If
- Production function exponents
- If
- Production function exponents
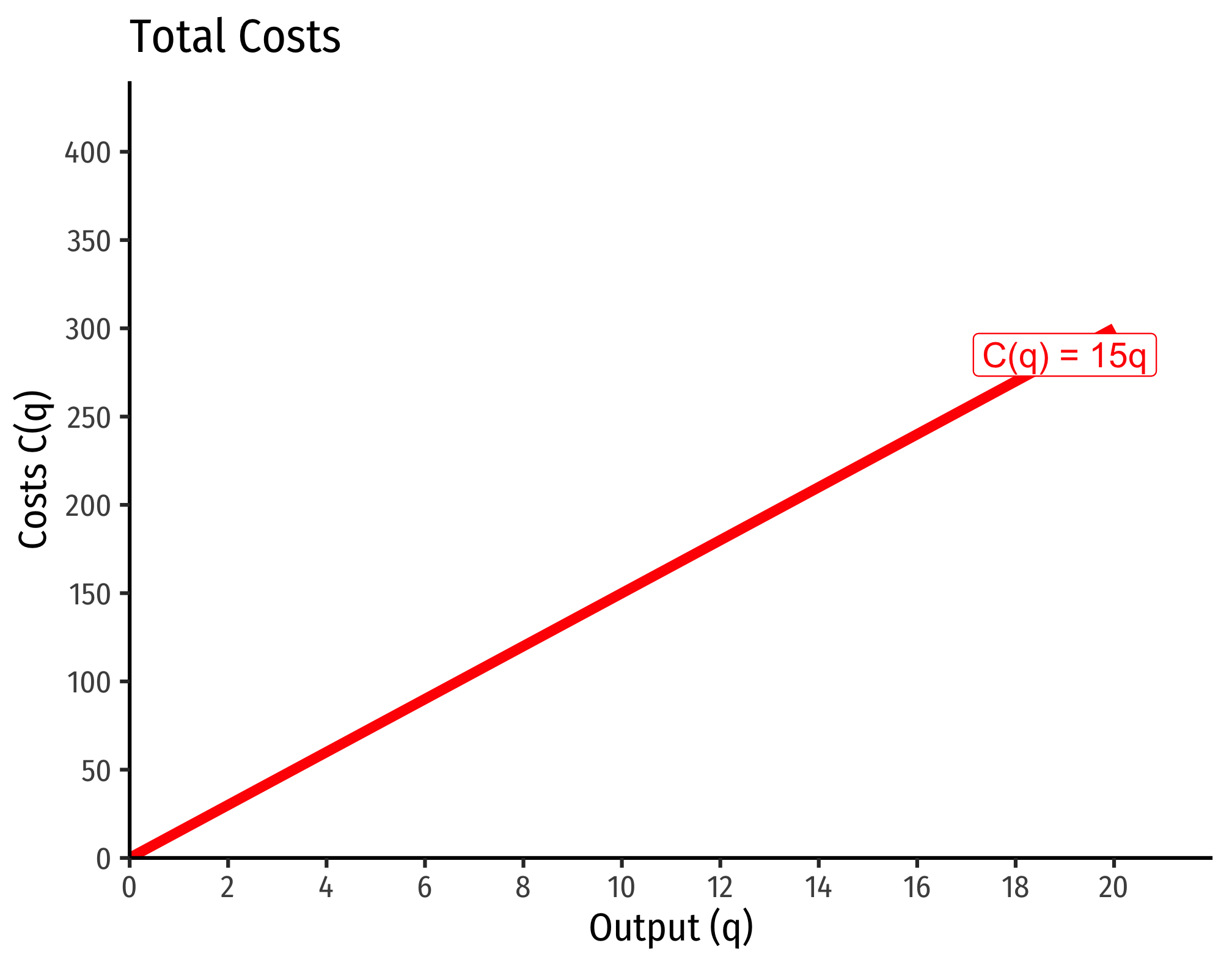
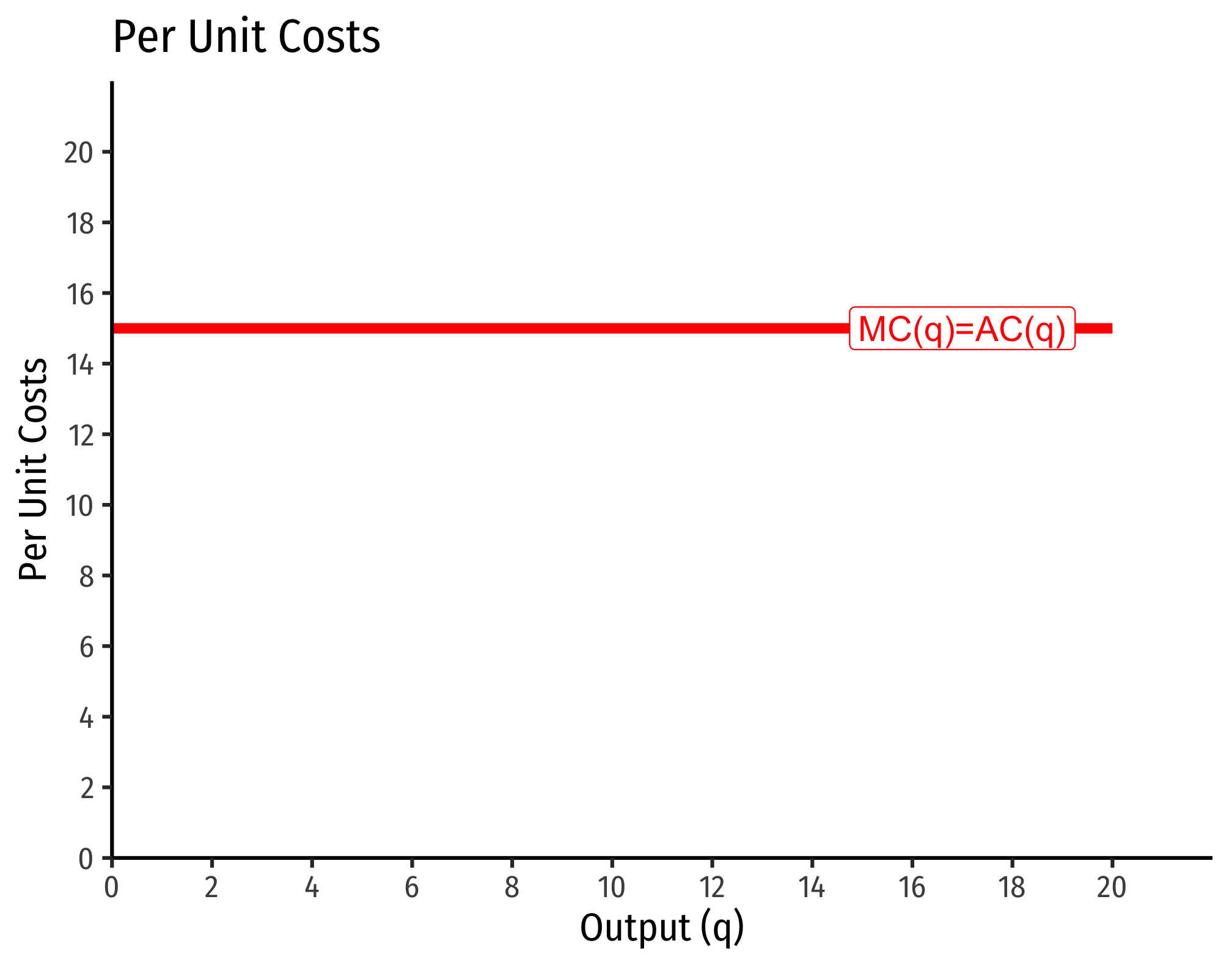
Example (Constant Returns)
Let
Consider input prices of
That is, total costs (at those given input prices, and technology) is equal to 15 times the output level,
Marginal costs would be
Average costs would be
Example (Decreasing Returns)
Let
If
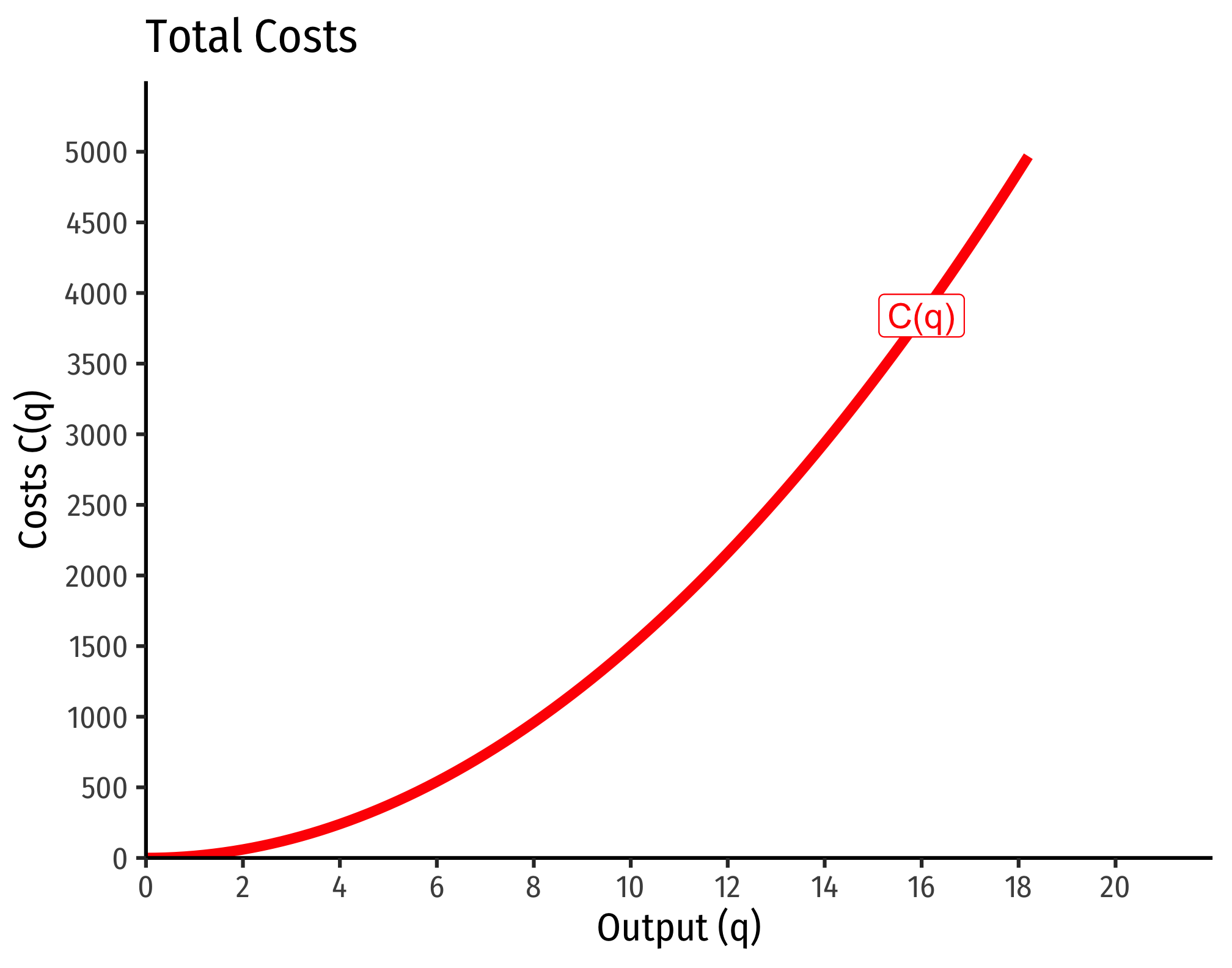
Marginal costs would be
Average costs would be