+ - 0:00:00
Notes for current slide
Notes for next slide

1.4 — Utility Maximization

ECON 306 • Microeconomic Analysis • Fall 2022

Ryan Safner
Associate Professor of Economics
safner@hood.edu
ryansafner/microF22
microF22.classes.ryansafner.com

Constrained Optimization

Constrained Optimization I

  • We model most situations as a constrained optimization problem:

  • People optimize: make tradeoffs to achieve their objective as best as they can

  • Subject to constraints: limited resources (income, time, attention, etc)

Constrained Optimization II

  • One of the most generally useful mathematical models

  • Endless applications: how we model nearly every decision-maker

consumer, business firm, politician, judge, bureaucrat, voter, dictator, pirate, drug cartel, drug addict, parent, child, etc

  • Key economic skill: recognizing how to apply the model to a situation

Remember!

Constrained Optimization III

  • All constrained optimization models have three moving parts:

Constrained Optimization III

  • All constrained optimization models have three moving parts:
  1. Choose: < some alternative >

Constrained Optimization III

  • All constrained optimization models have three moving parts:

  1. Choose: < some alternative >

  2. In order to maximize: < some objective >

Constrained Optimization III

  • All constrained optimization models have three moving parts:

  1. Choose: < some alternative >

  2. In order to maximize: < some objective >

  3. Subject to: < some constraints >

Constrained Optimization: Example I

Example: A Hood student picking courses hoping to achieve the highest GPA while getting an Econ major.

  1. Choose:

  2. In order to maximize:

  3. Subject to:

Constrained Optimization: Example II

Example: How should FedEx plan its delivery route?

  1. Choose:

  2. In order to maximize:

  3. Subject to:

Constrained Optimization: Example III

Example: The U.S. government wants to remain economically competitive but reduce emissions by 25%.

  1. Choose:

  2. In order to maximize:

  3. Subject to:

Constrained Optimization: Example IV

Example: How do elected officials make decisions in politics?

  1. Choose:

  2. In order to maximize:

  3. Subject to:

The Utility Maximization Problem

  • The individual's utility maximization problem we've been modeling, finally, is:

  1. Choose: < a consumption bundle >

  2. In order to maximize: < utility >

  3. Subject to: < income and market prices >

The Utility Maximization Problem: Tools

  • We now have the tools to understand individual choices:

  • Budget constraint: individual’s constraints of income and market prices

    • How market trades off between goods
    • Marginal cost (of good \(x\), in terms of \(y)\)

  • Utility function: individual’s objective to maximize, based on their preferences

    • How individual trades off between goods
    • Marginal benefit (of good \(x\), in terms of \(y)\)

The Utility Maximization Problem: Verbally

  • The individual's constrained optimization problem:

choose a bundle of goods to maximize utility, subject to income and market prices

The Utility Maximization Problem: Mathematically

$$\max_{x,y \geq0} u(x,y)$$ $$s.t. p_xx+p_yy=m$$

  • This requires calculus to solve.† We will look at graphs instead!

† See the mathematical appendix in today's class notes on how to solve it with calculus, and an example.

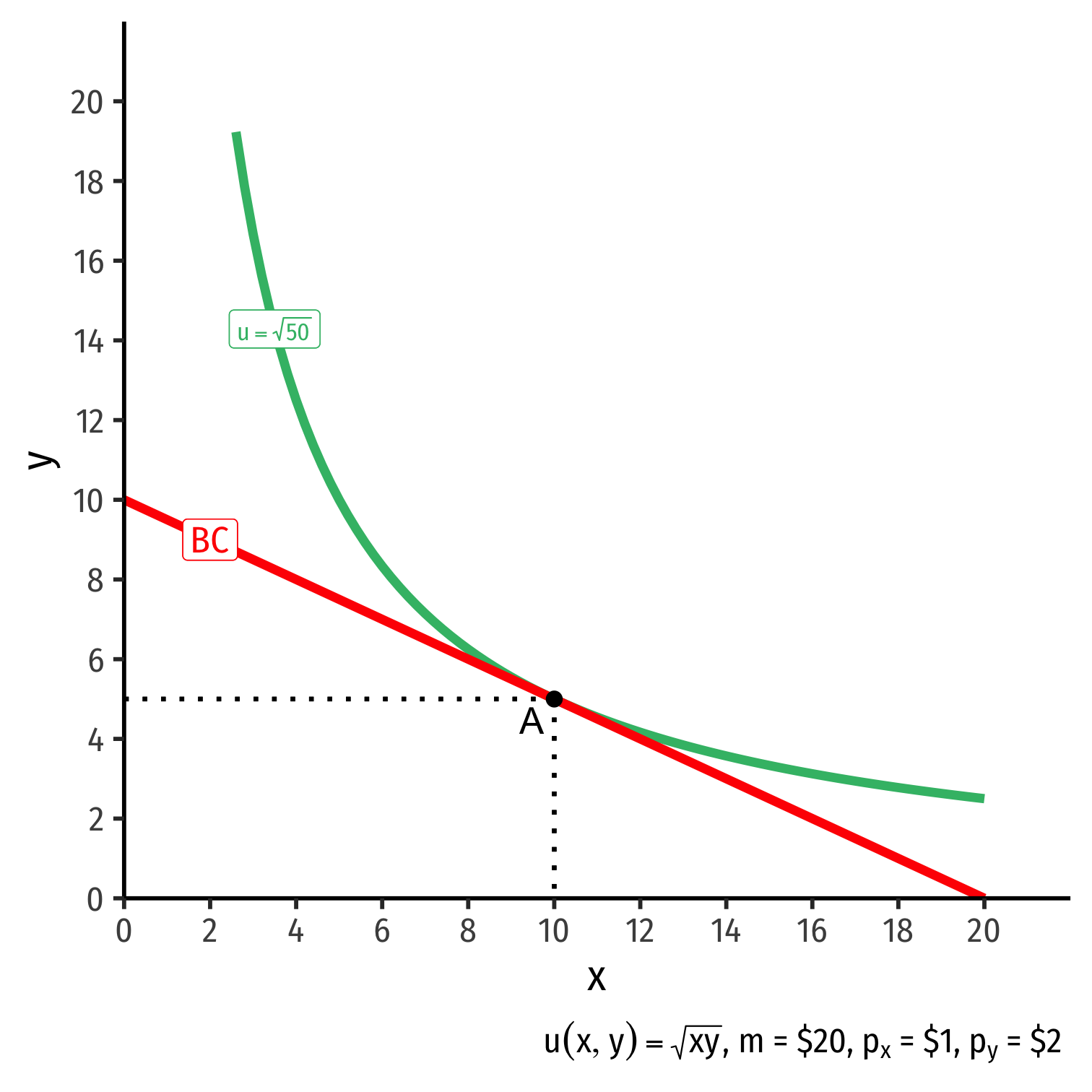
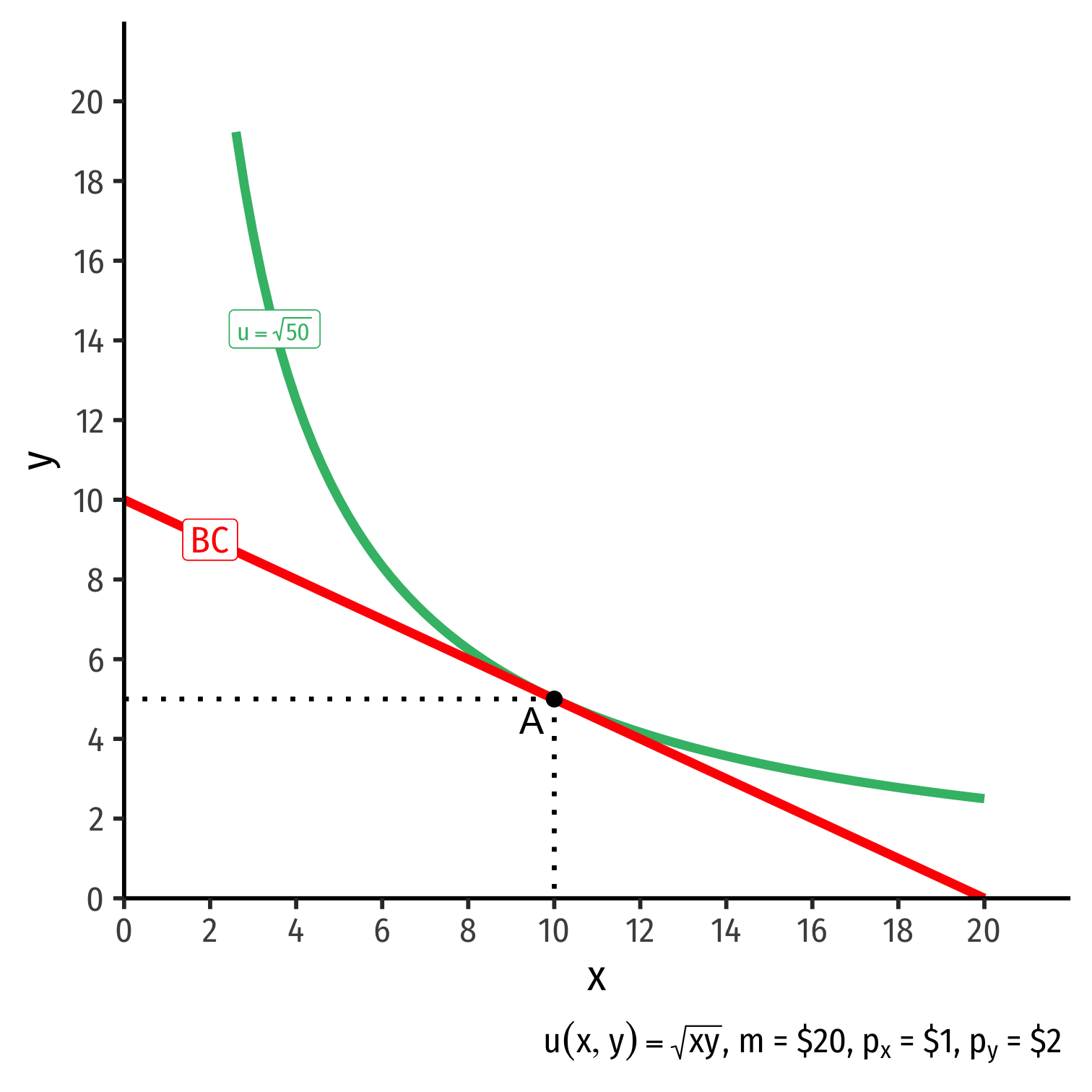
The Individual's Optimum: Graphically

  • Graphical solution: Highest indifference curve tangent to budget constraint
    • Bundle A!

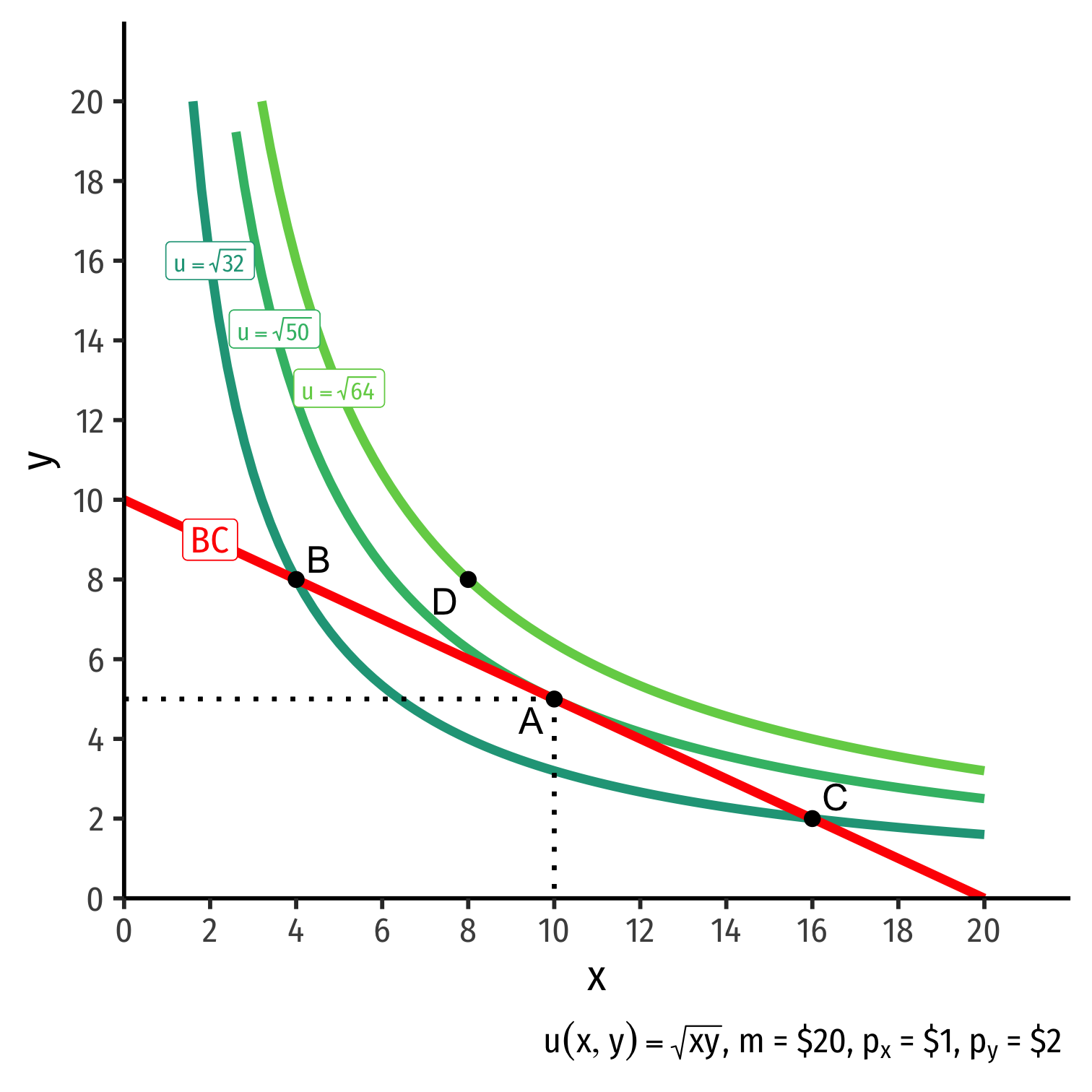
The Individual's Optimum: Graphically

  • Graphical solution: Highest indifference curve tangent to budget constraint

    • Bundle A!

  • B or C spend all income, but a better combination exists

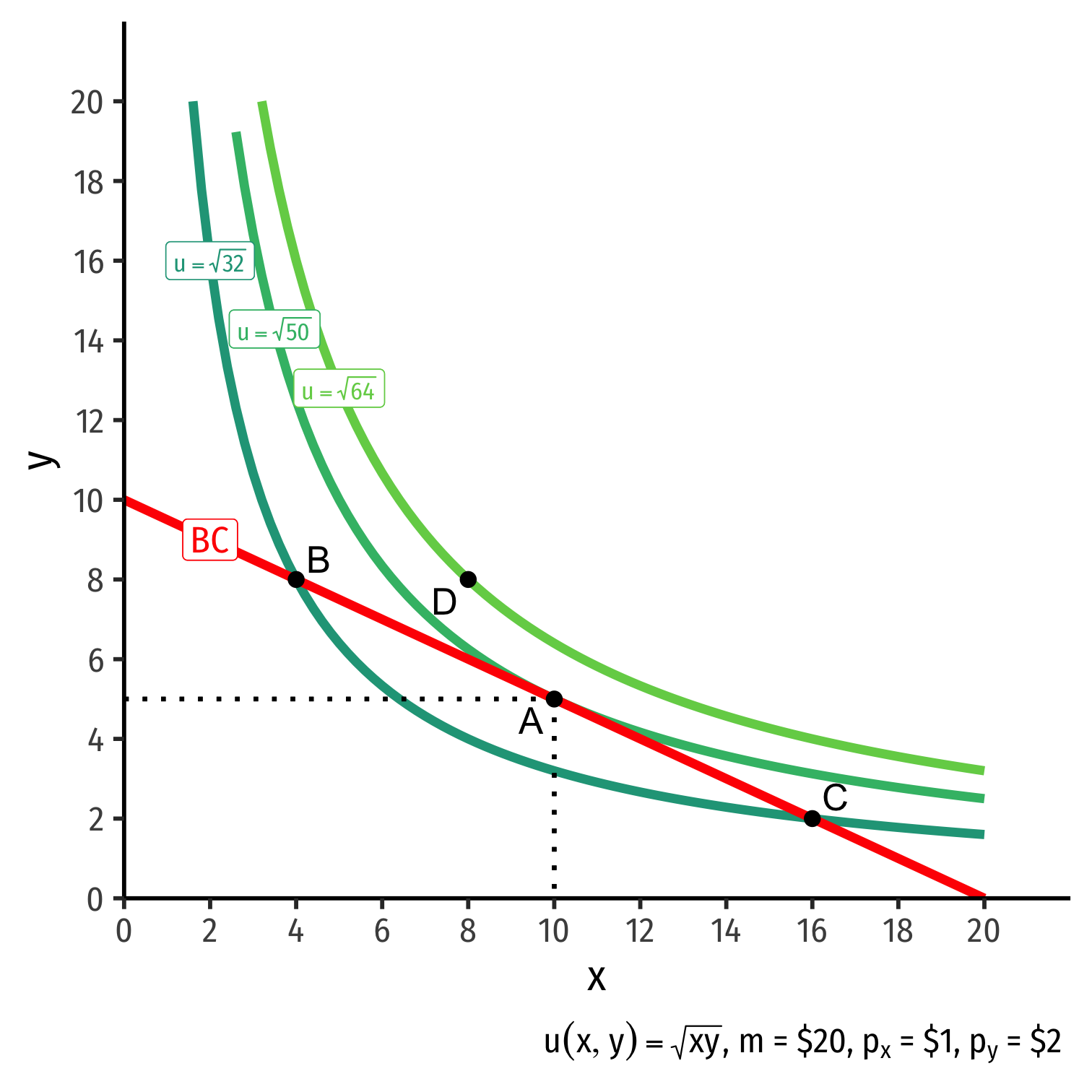
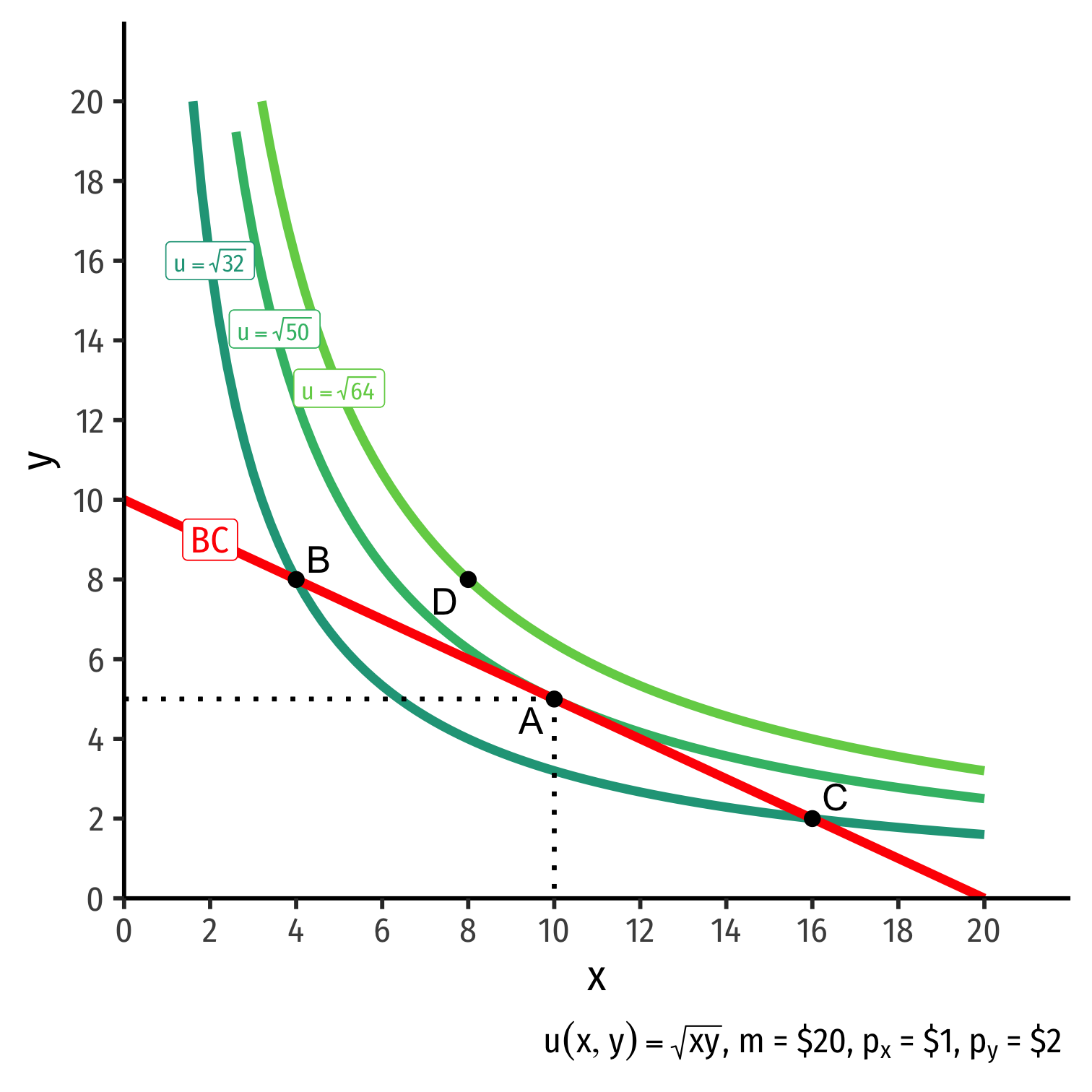
The Individual's Optimum: Graphically

  • Graphical solution: Highest indifference curve tangent to budget constraint

    • Bundle A!

  • B or C spend all income, but a better combination exists

  • D is higher utility, but not affordable at current income & prices

The Individual's Optimum: Why Not B?

$$\begin{align*} \color{#047806}{\text{indiff. curve slope}} &> \color{#D7250E}{\text{budget constr. slope}} \\ \end{align*}$$

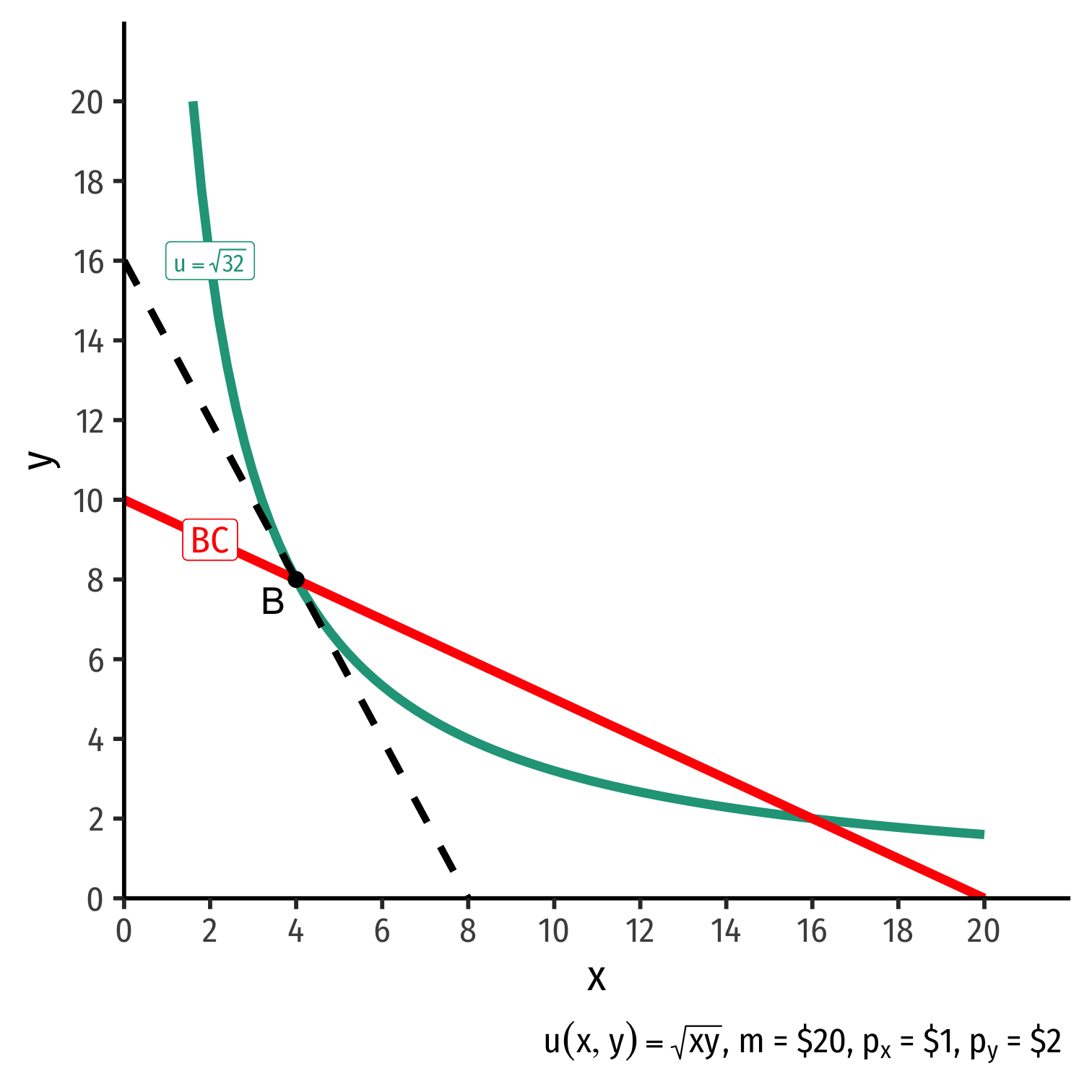
The Individual's Optimum: Why Not B?

$$\begin{align*} \color{#047806}{\text{indiff. curve slope}} &> \color{#D7250E}{\text{budget constr. slope}} \\ \color{#047806}{\frac{MU_x}{MU_y}} &> \color{#D7250E}{\frac{p_x}{p_y}} \\ \color{#047806}{2} &> \color{#D7250E}{0.5} \\\end{align*}$$

  • Consumer views MB of \(x\) is 2 units of \(y\)

    • Consumer’s “exchange rate:” 2Y:1X

  • Market-determined MC of \(x\) is 0.5 units of \(y\)

    • Market exchange rate is 0.5Y:1X

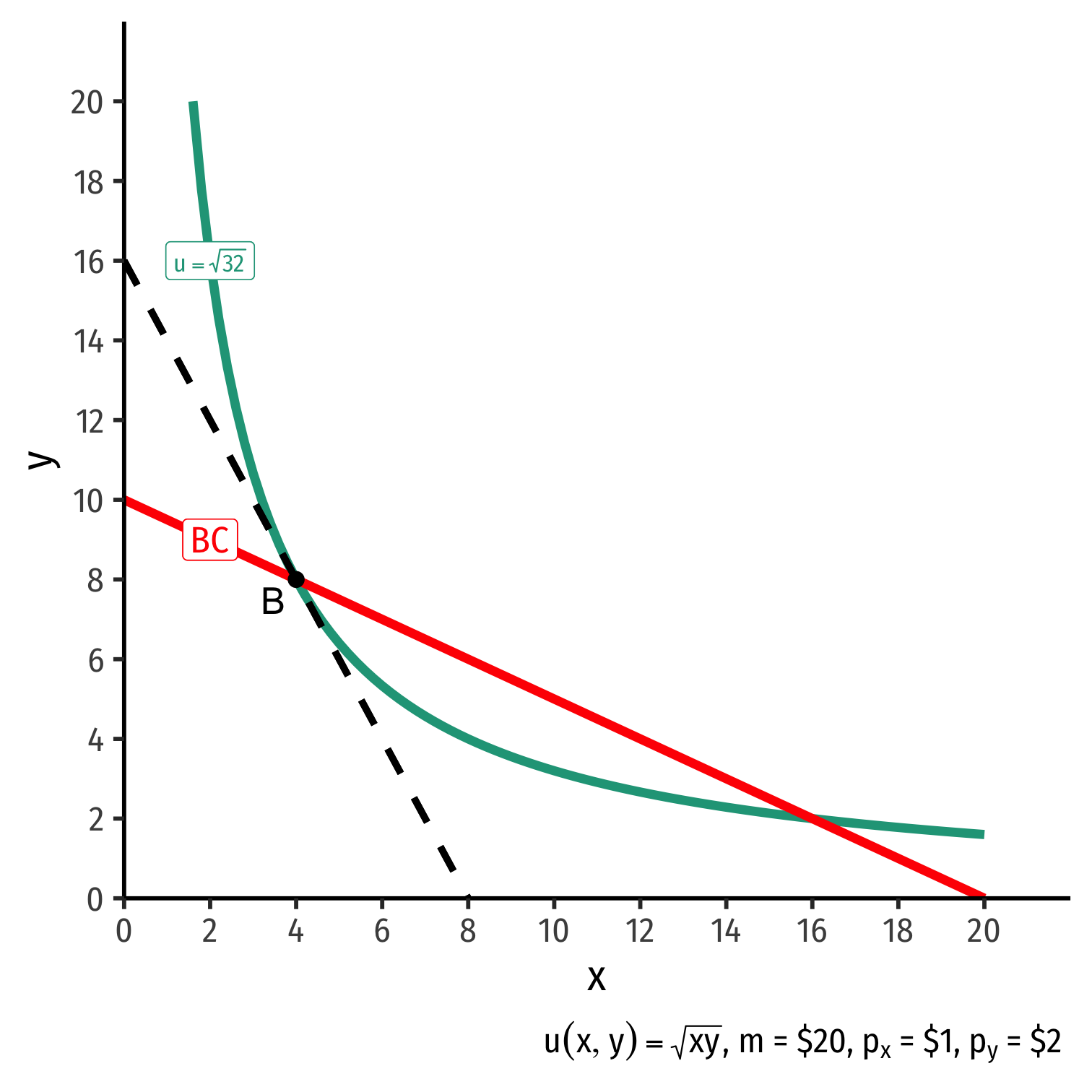
The Individual's Optimum: Why Not B?

$$\begin{align*} \color{#047806}{\text{indiff. curve slope}} &> \color{#D7250E}{\text{budget constr. slope}} \\ \color{#047806}{\frac{MU_x}{MU_y}} &> \color{#D7250E}{\frac{p_x}{p_y}} \\ \color{#047806}{2} &> \color{#D7250E}{0.5} \\\end{align*}$$

  • Consumer views MB of \(x\) is 2 units of \(y\)

    • Consumer’s “exchange rate:” 2Y:1X

  • Market-determined MC of \(x\) is 0.5 units of \(y\)

    • Market exchange rate is 0.5Y:1X

  • Can spend less on y, more on x for more utility!

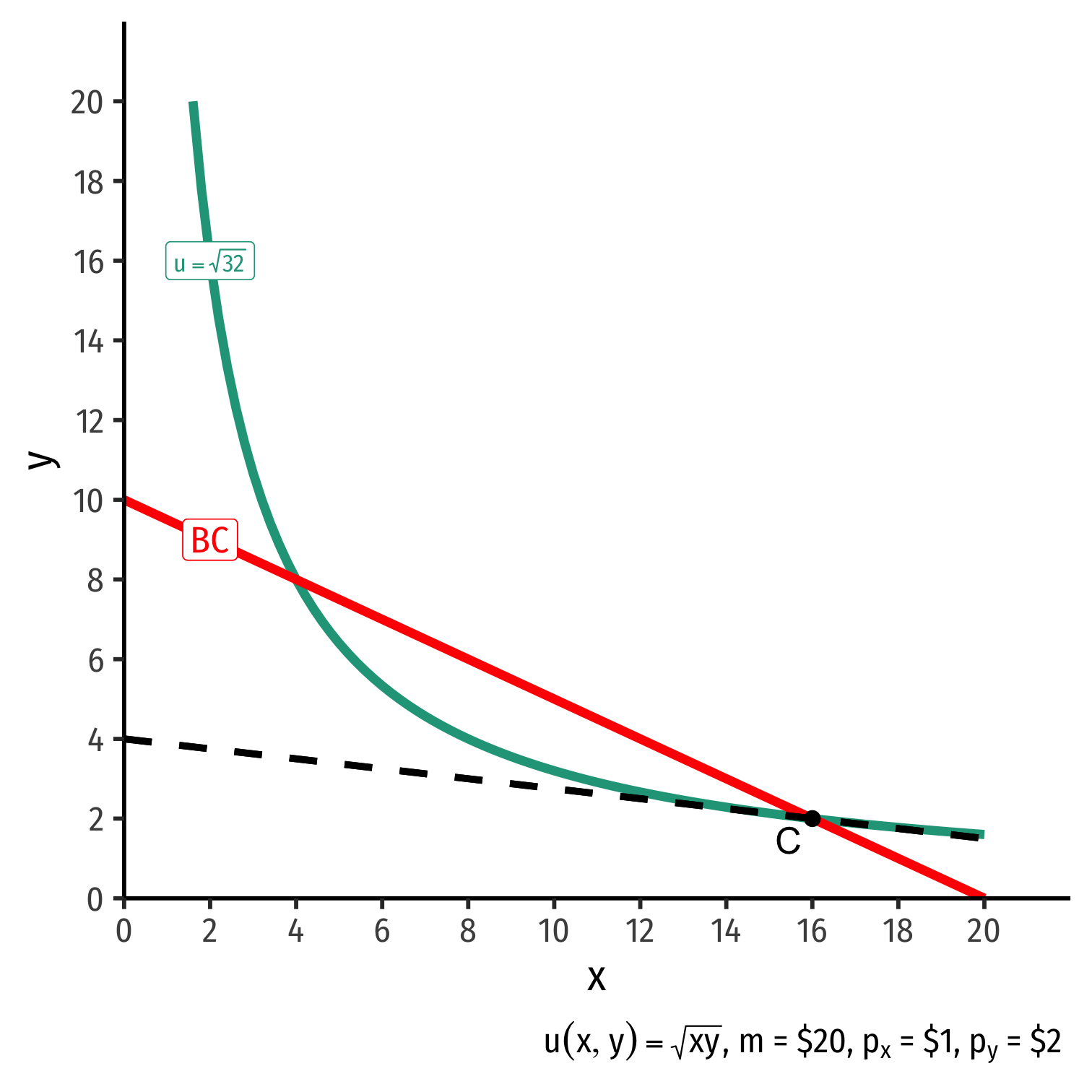
The Individual's Optimum: Why Not C?

$$\begin{align*} \color{#047806}{\text{indiff. curve slope}} &< \color{#D7250E}{\text{budget constr. slope}} \\ \\\end{align*}$$

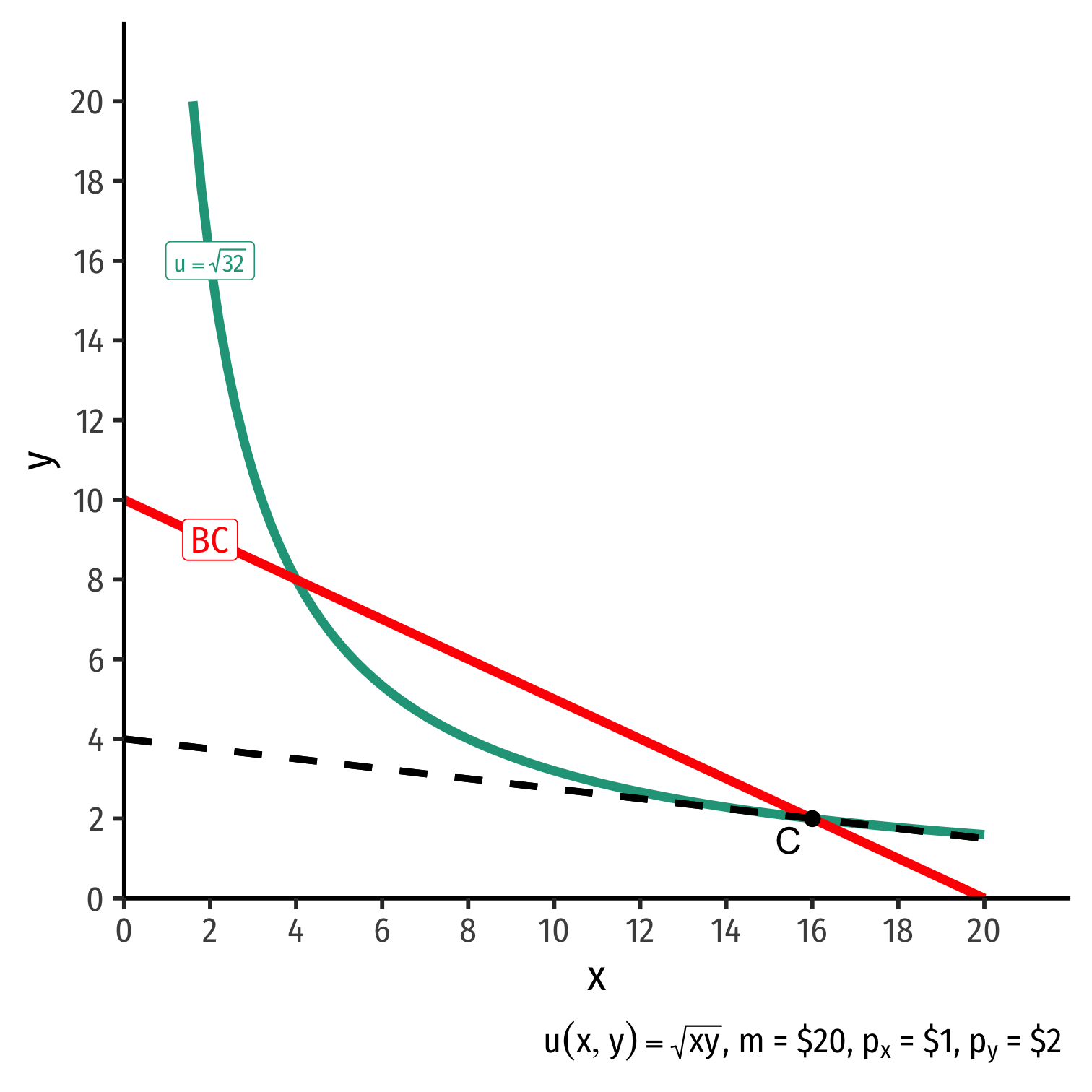
The Individual's Optimum: Why Not C?

$$\begin{align*} \color{#047806}{\text{indiff. curve slope}} &< \color{#D7250E}{\text{budget constr. slope}} \\ \color{#047806}{\frac{MU_x}{MU_y}} &< \color{#D7250E}{\frac{p_x}{p_y}} \\ \color{#047806}{0.125} &< \color{#D7250E}{0.5} \\\end{align*}$$

  • Consumer views MB of \(x\) is 0.125 units of \(y\)

    • Consumer’s “exchange rate:” 0.125Y:1X

  • Market-determined MC of \(x\) is 0.5 units of \(y\)

    • Market exchange rate is 0.5Y:1X

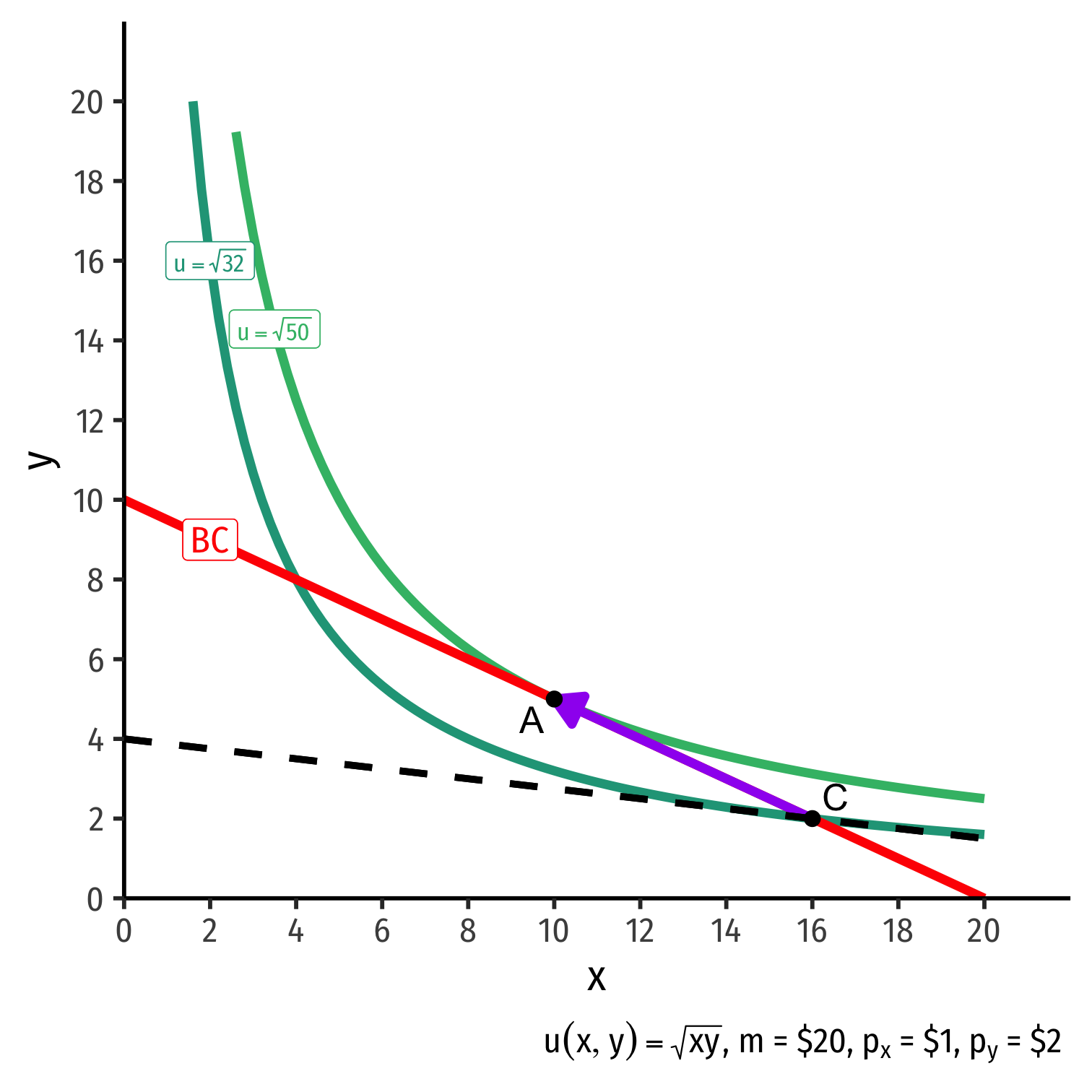
The Individual's Optimum: Why Not C?

$$\begin{align*} \color{#047806}{\text{indiff. curve slope}} &< \color{#D7250E}{\text{budget constr. slope}} \\ \color{#047806}{\frac{MU_x}{MU_y}} &< \color{#D7250E}{\frac{p_x}{p_y}} \\ \color{#047806}{0.125} &< \color{#D7250E}{0.5} \\\end{align*}$$

  • Consumer views MB of \(x\) is 0.125 units of \(y\)

    • Consumer’s “exchange rate:” 0.125Y:1X

  • Market-determined MC of \(x\) is 0.5 units of \(y\)

    • Market exchange rate is 0.5Y:1X

  • Can spend less on y, more on x for more utility!

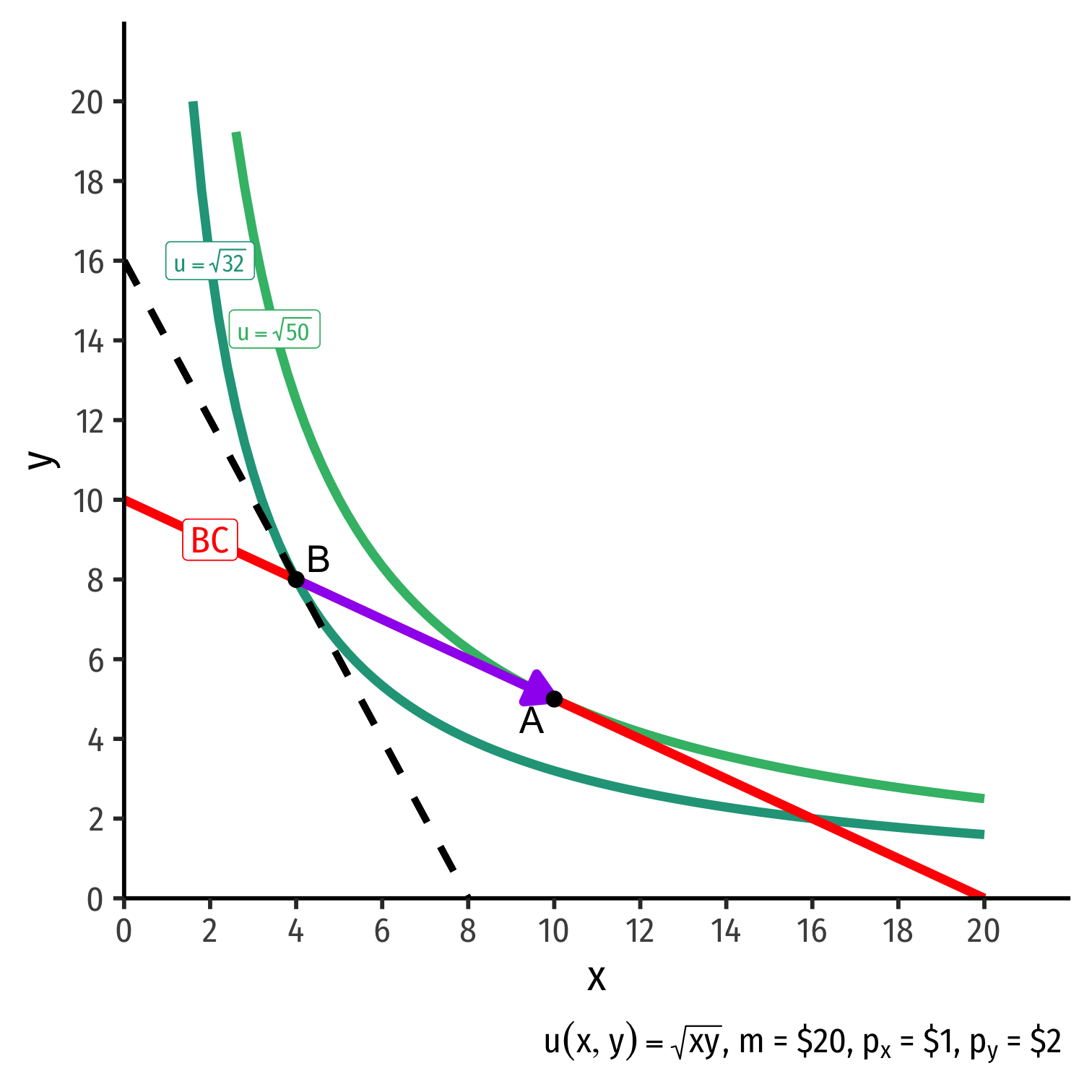
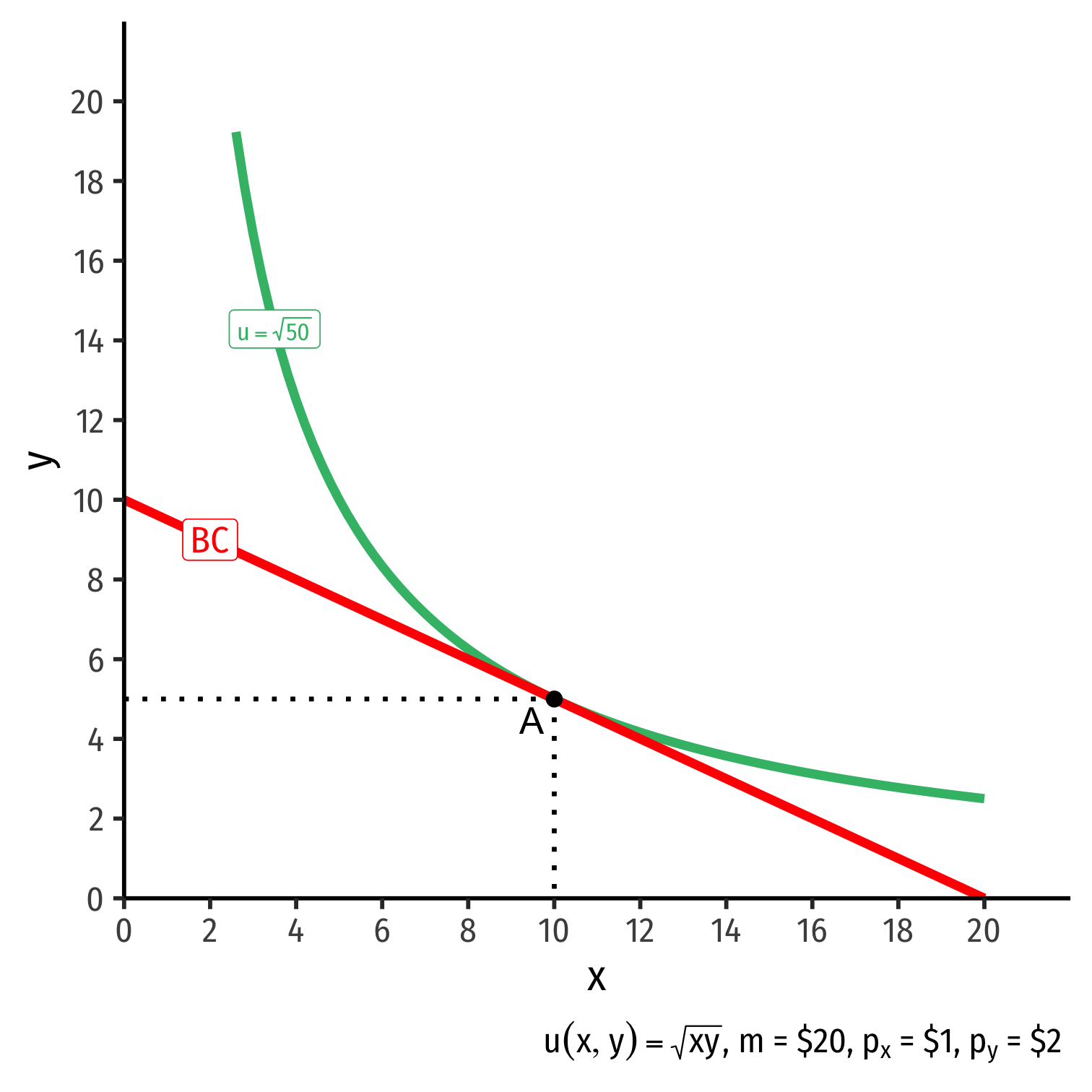
The Individual's Optimum: Why A?

$$\begin{align*} \color{#047806}{\text{indiff. curve slope}} &= \color{#D7250E}{\text{budget constr. slope}} \\\end{align*}$$

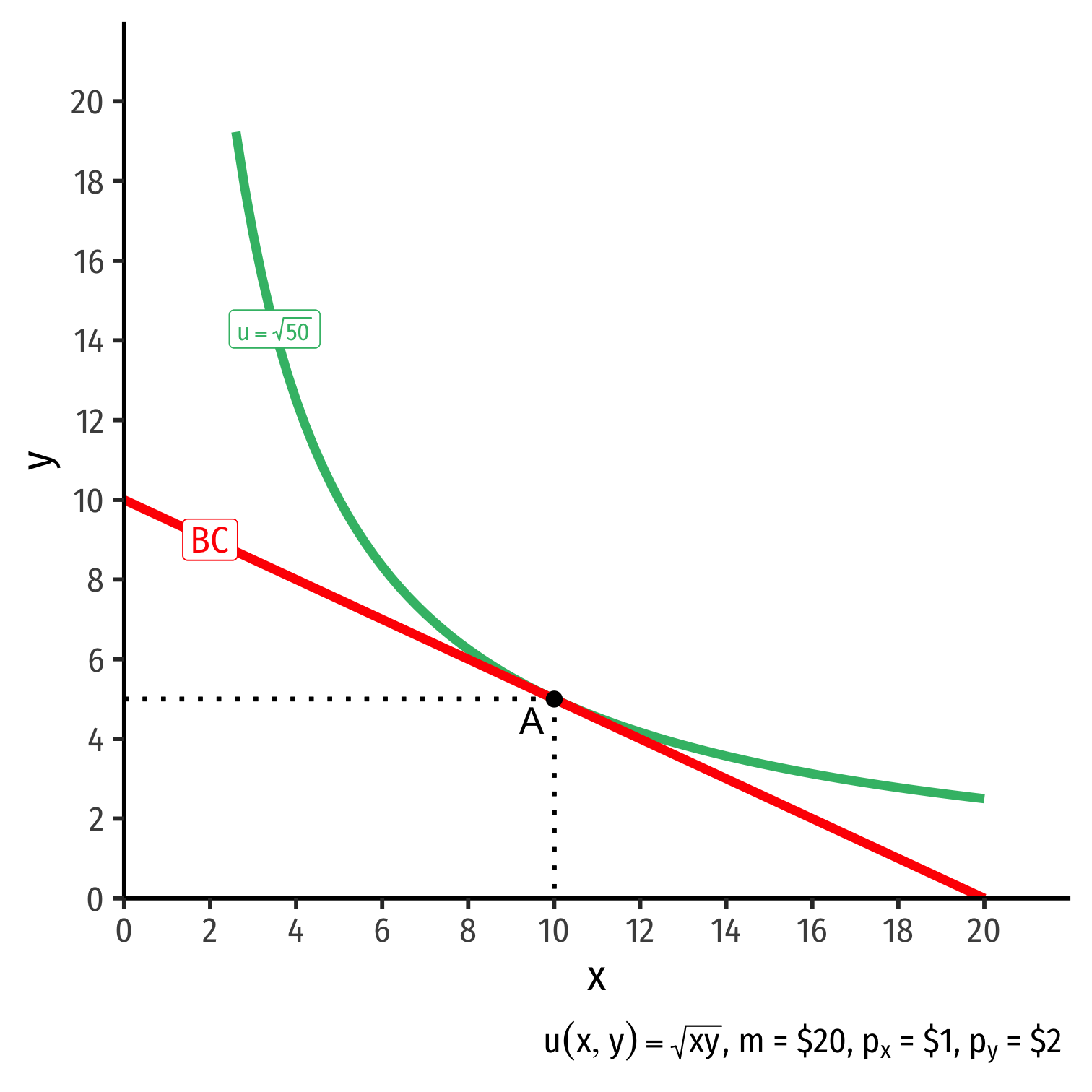
The Individual's Optimum: Why A?

$$\begin{align*} \color{#047806}{\text{indiff. curve slope}} &= \color{#D7250E}{\text{budget constr. slope}} \\ \color{#047806}{\frac{MU_x}{MU_y}} &= \color{#D7250E}{\frac{p_x}{p_y}} \\ \color{#047806}{0.5} &= \color{#D7250E}{0.5} \\\end{align*}$$

  • Marginal benefit = Marginal cost

    • Consumer exchanges at same rate as market

  • No other combination of (x,y) exists that could increase utility!†

† At current income and market prices!

The Individual's Optimum: Two Equivalent Rules

Rule 1

$$\frac{MU_x}{MU_y} = \frac{p_x}{p_y}$$

  • Easier for calculation (slopes)

The Individual's Optimum: Two Equivalent Rules

Rule 1

$$\frac{MU_x}{MU_y} = \frac{p_x}{p_y}$$

  • Easier for calculation (slopes)

Rule 2

$$\frac{MU_x}{p_x} = \frac{MU_y}{p_y}$$

  • Easier for intuition (next slide)

The Individual's Optimum: The Equimarginal Rule

$$\frac{MU_x}{p_x} = \frac{MU_y}{p_y} = \cdots = \frac{MU_n}{p_n}$$

  • Equimarginal Rule: consumption is optimized where the marginal utility per dollar spent is equalized across all \(n\) possible goods/decisions

  • Always choose an option that gives higher marginal utility (e.g. if \(MU_x < MU_y)\), consume more \(y\)!

    • But each option has a different price, so weight each option by its price, hence \(\frac{MU_x}{p_x}\)

An Optimum, By Definition

  • Any optimum in economics: no better alternatives exist under current constraints

  • No possible change in your consumption that would increase your utility

Practice I

Example: You can get utility from consuming bags of Almonds \((a)\) and bunches of Bananas \((b)\), according to the utility function:

$$\begin{align*} u(a,b)&=ab\\ MU_a&=b \\ MU_b&=a \\ \end{align*}$$

You have an income of $50, the price of Almonds is $10, and the price of Bananas is $2. Put Almonds on the horizontal axis and Bananas on the vertical axis.

  1. What is your utility-maximizing bundle of Almonds and Bananas?
  2. How much utility does this provide? [Does the answer to this matter?]

Practice II, Cobb-Douglas!

Example: You can get utility from consuming Burgers \((b)\) and Fries \((f)\), according to the utility function:

$$\begin{align*} u(b,f)&=\sqrt{bf} \\ MU_b&=0.5b^{-0.5}f^{0.5} \\ MU_f&=0.5b^{0.5}f^{-0.5} \\ \end{align*}$$

You have an income of $20, the price of Burgers is $5, and the price of Fries is $2. Put Burgers on the horizontal axis and Fries on the vertical axis.

  1. What is your utility-maximizing bundle of Burgers and Fries?
  2. How much utility does this provide?

Constrained Optimization

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
oTile View: Overview of Slides
Esc Back to slideshow