1.3 — Preferences
ECON 306 • Microeconomic Analysis • Fall 2022
Ryan Safner
Associate Professor of Economics
safner@hood.edu
ryansafner/microF22
microF22.classes.ryansafner.com
Preferences
Preferences I
- Which bundles are preferred over others?
Example: Between two bundles of (x,y):
a=(4,12) or b=(6,12)

Preferences II
- We will allow three possible answers:

Preferences II
- We will allow three possible answers:
- a≻b: (Strictly) prefer a over b

Preferences II
- We will allow three possible answers:
a≻b: (Strictly) prefer a over b
a≺b: (Strictly) prefer b over a

Preferences II
- We will allow three possible answers:
a≻b: (Strictly) prefer a over b
a≺b: (Strictly) prefer b over a
a∼b: Indifferent between a and b

Preferences II
- We will allow three possible answers:
a≻b: (Strictly) prefer a over b
a≺b: (Strictly) prefer b over a
a∼b: Indifferent between a and b
- Preferences are a list of all such comparisons between all bundles
See appendix in today's class page for more.

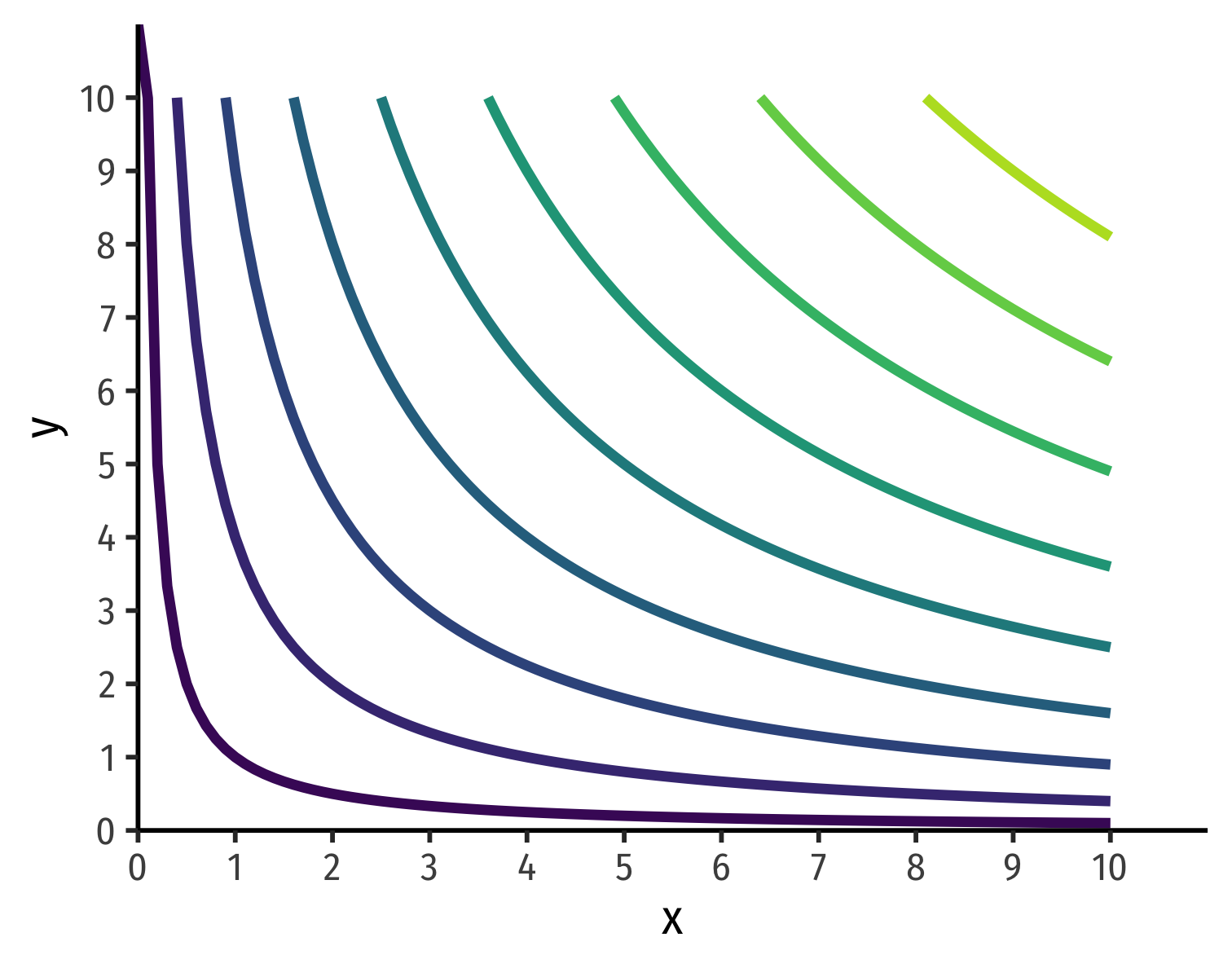
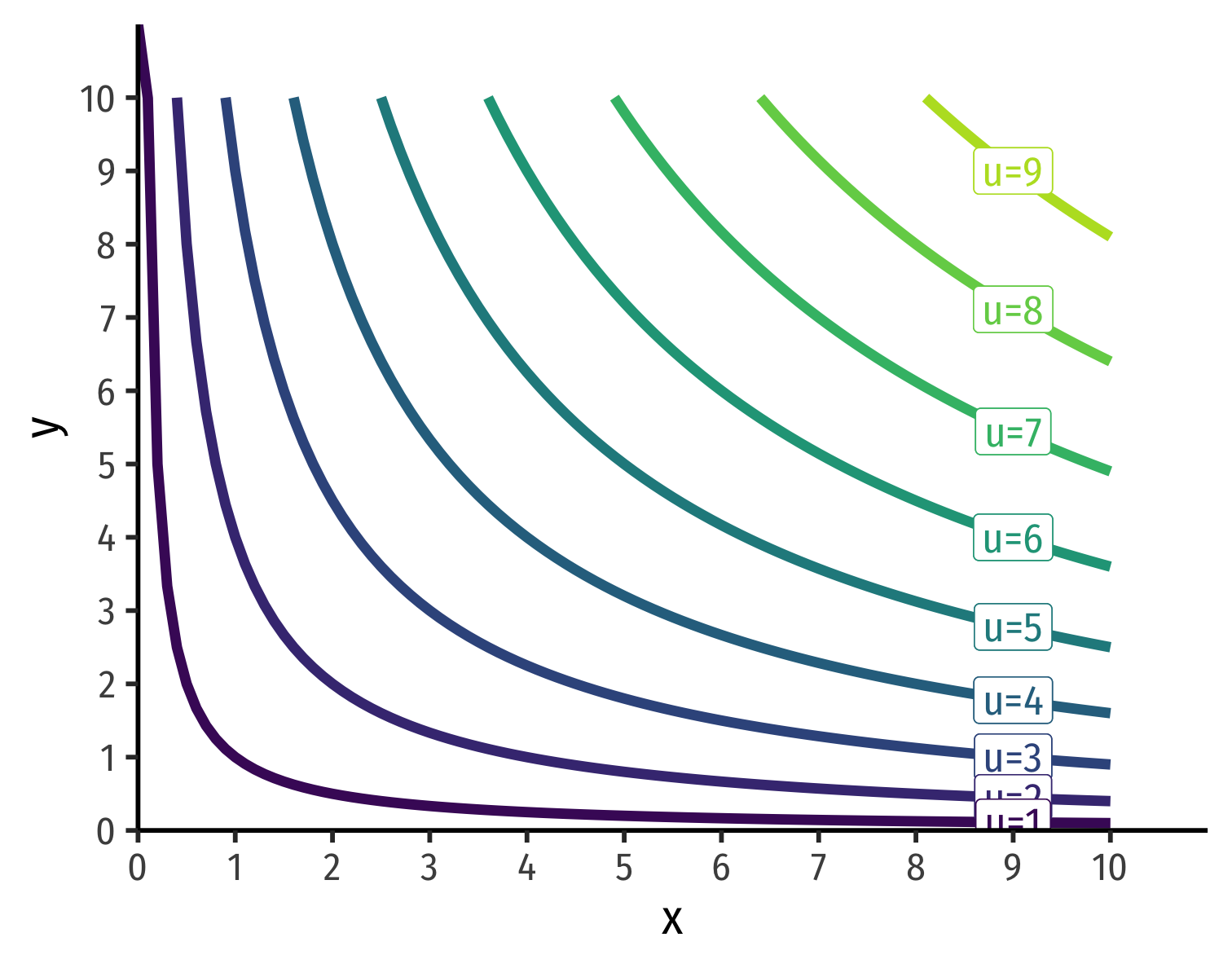
Indifference Curves
Mapping Preferences Graphically I
For each bundle, we now have 3 pieces of information:
- amount of x
- amount of y
- preference compared to other bundles
How to represent this information graphically?

Mapping Preferences Graphically II
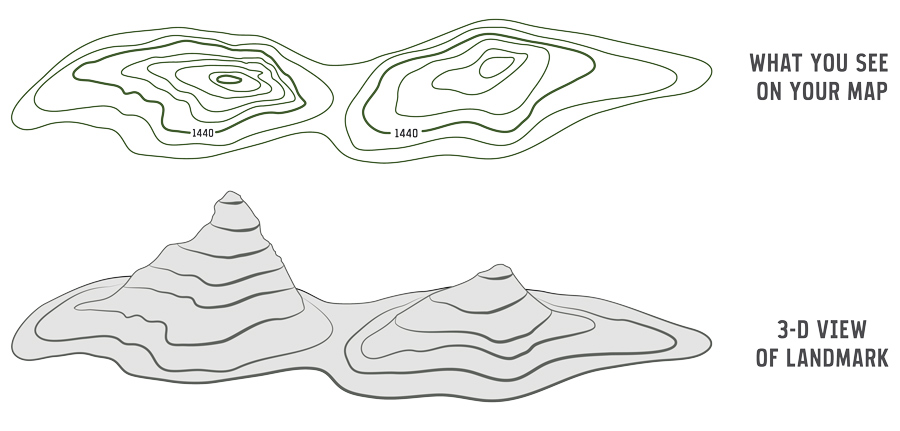
Cartographers have the answer for us
On a map, contour lines link areas of equal height
We will use “indifference curves” to link bundles of equal preference
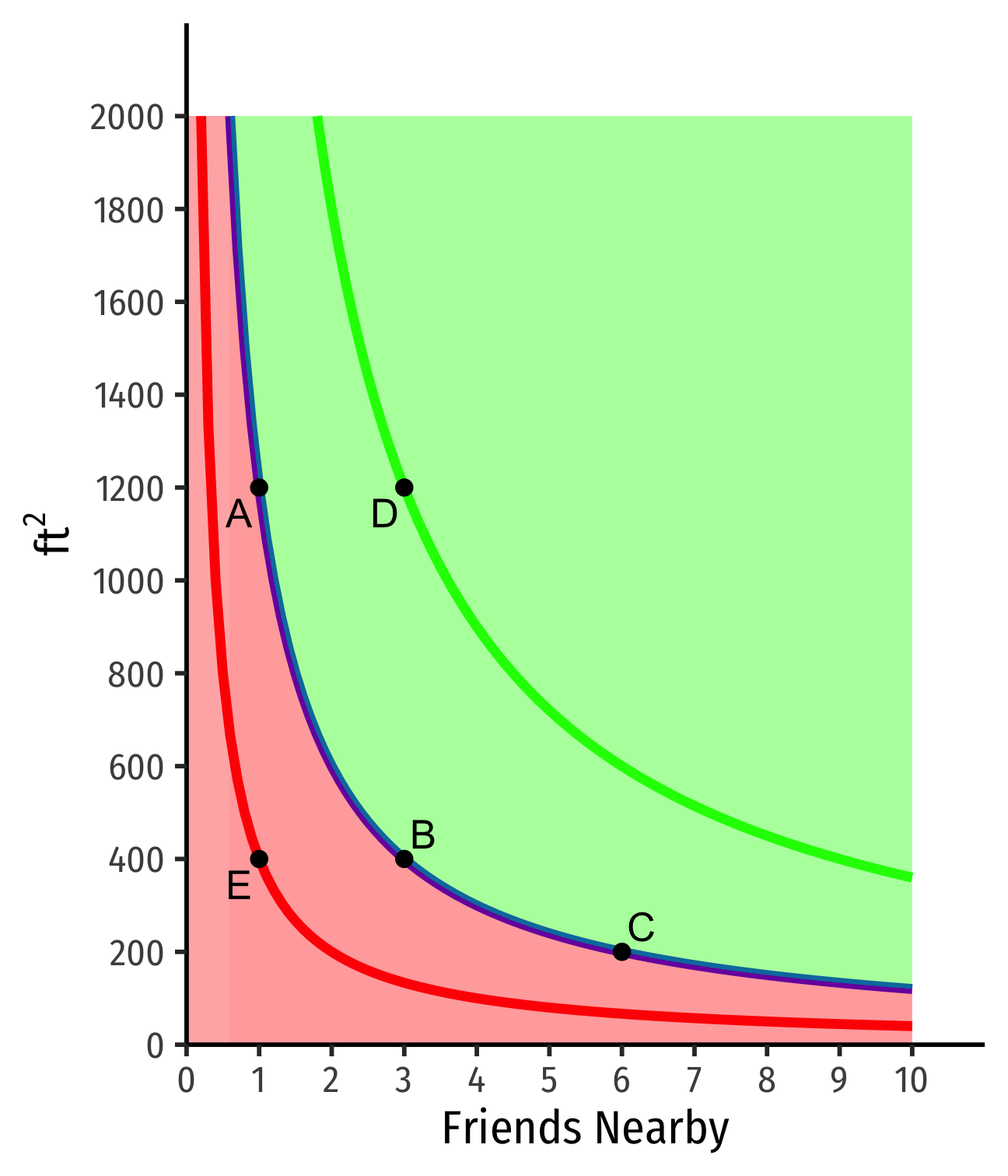
Indifference Curves: Example
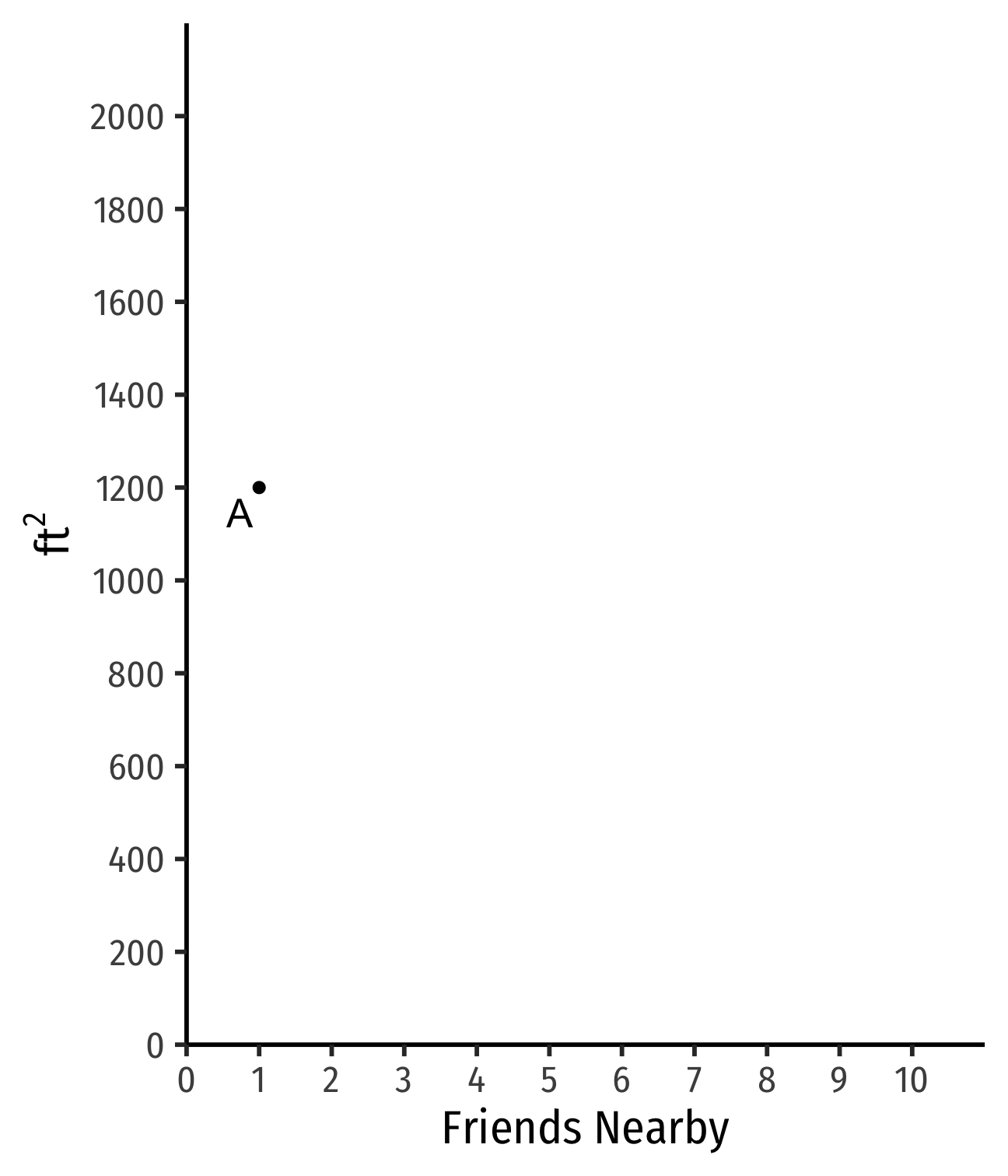
Example: Suppose you are hunting for an apartment. You value both the size of the apartment and the number of friends that live nearby.
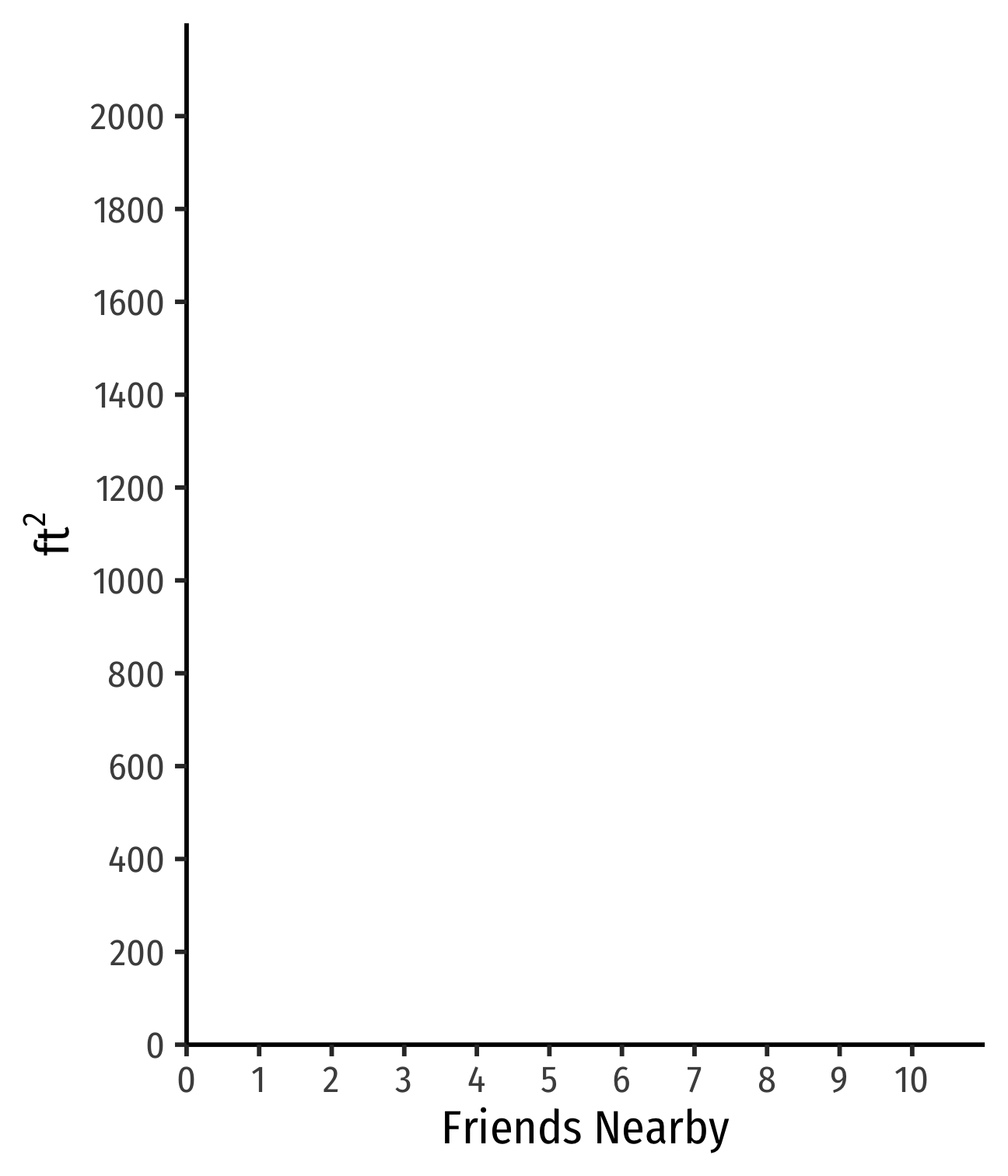
Indifference Curves: Example
Example: Suppose you are hunting for an apartment. You value both the size of the apartment and the number of friends that live nearby.
- Apt. A has 1 friend nearby and is 1,200 ft2
Indifference Curves: Example
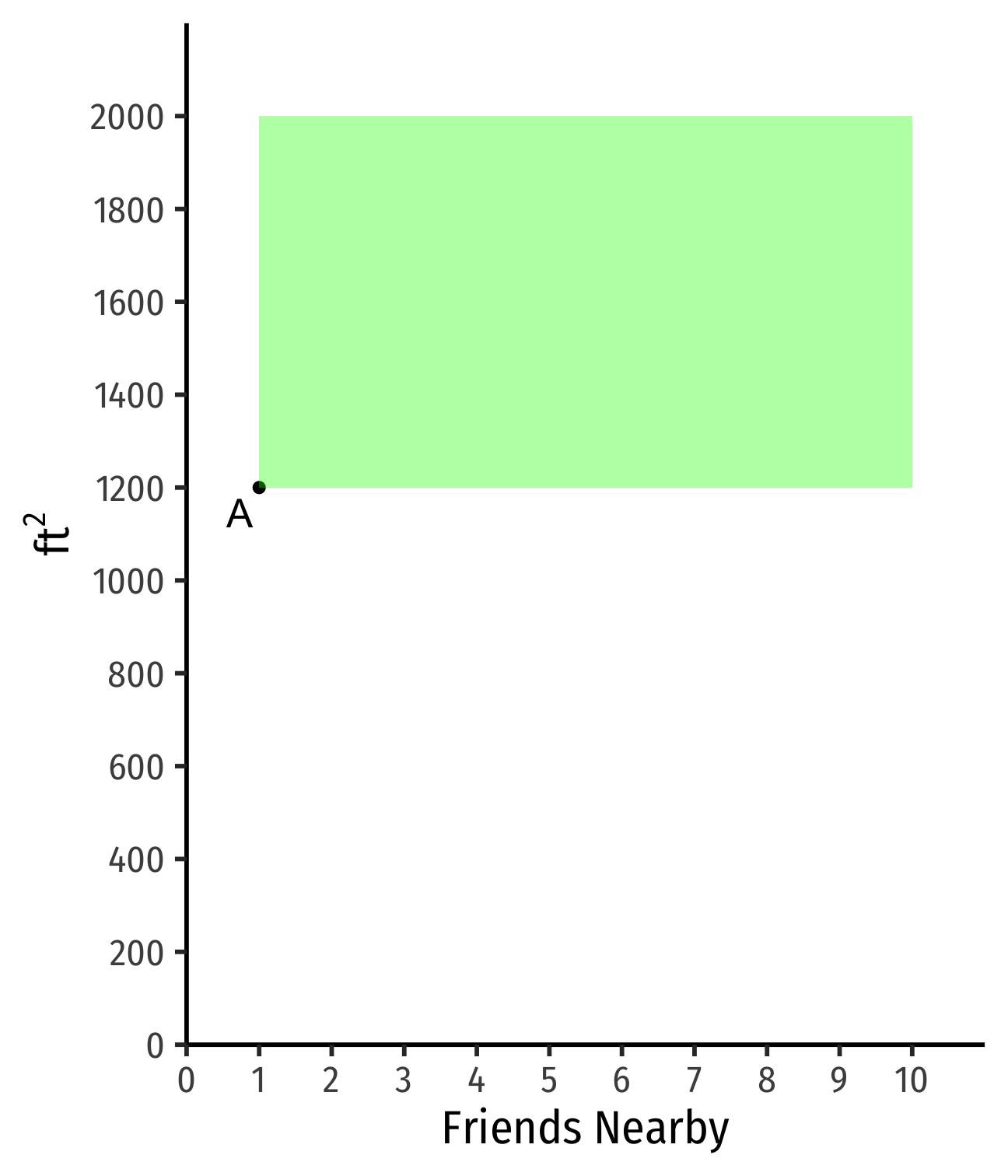
Example: Suppose you are hunting for an apartment. You value both the size of the apartment and the number of friends that live nearby.
- Apt. A has 1 friend nearby and is 1,200 ft2
- Apts that are larger and/or have more friends ≻A
Indifference Curves: Example
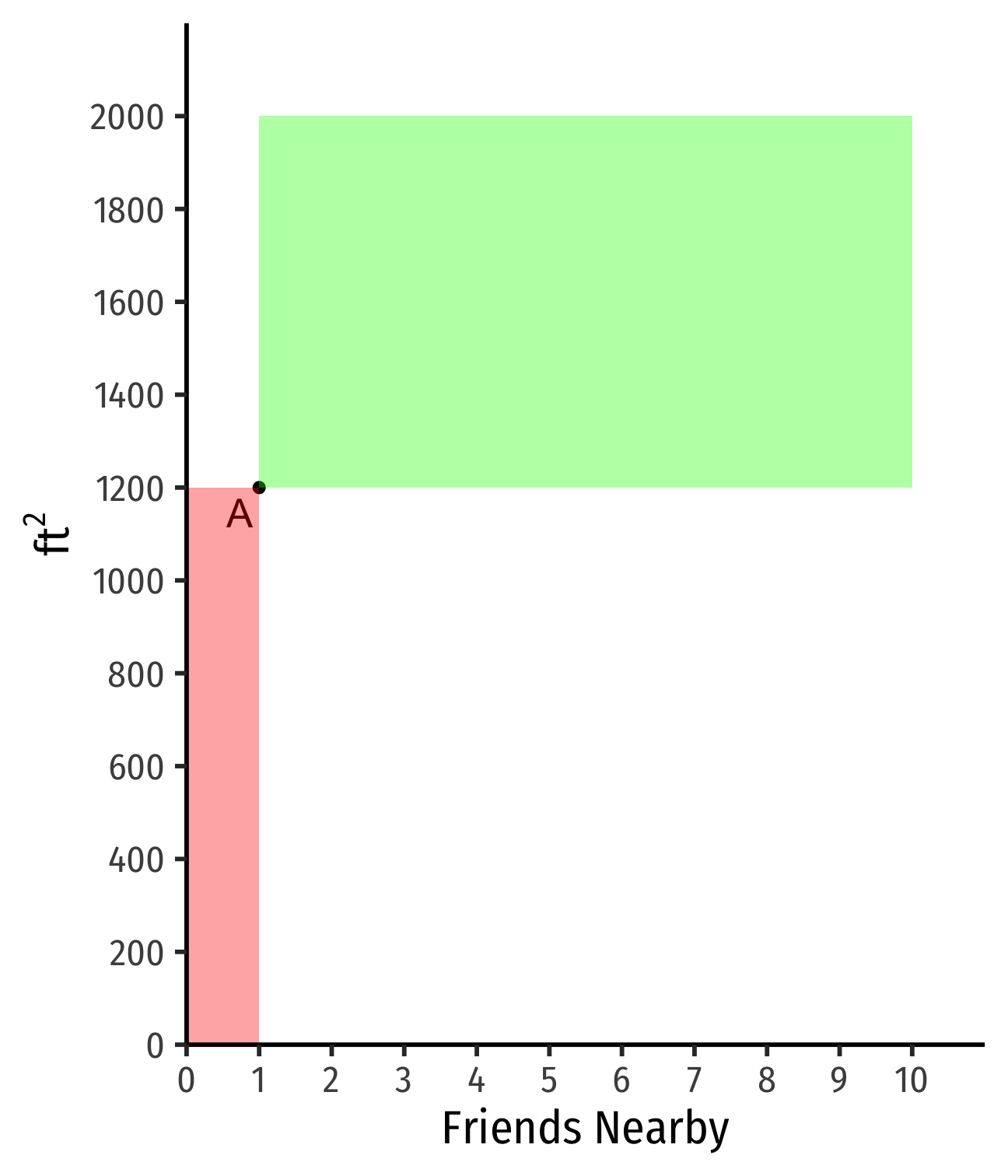
Example: Suppose you are hunting for an apartment. You value both the size of the apartment and the number of friends that live nearby.
- Apt. A has 1 friend nearby and is 1,200 ft2
- Apts that are larger and/or have more friends ≻A
- Apts that are smaller and/or have fewer friends ≺A
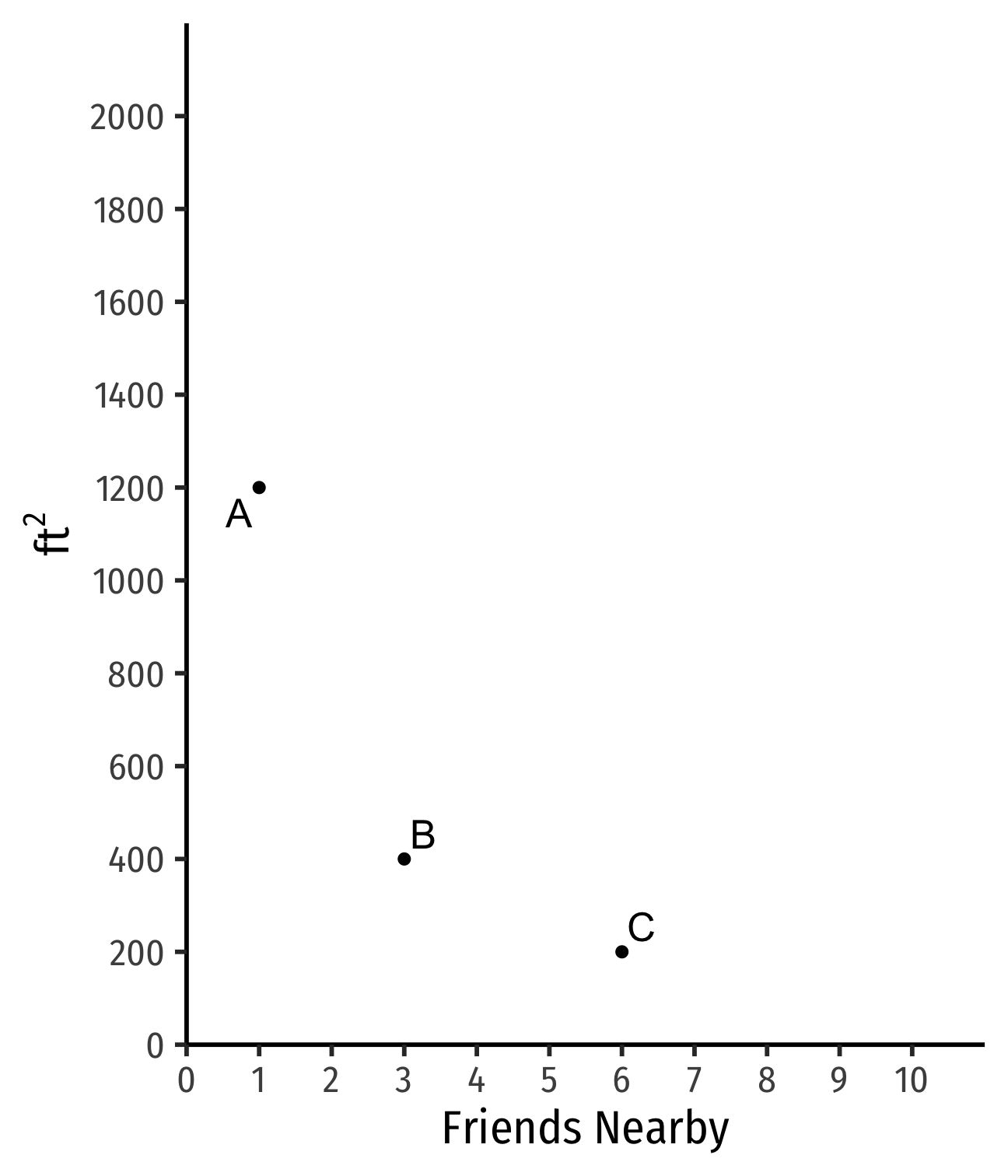
Indifference Curves: Example
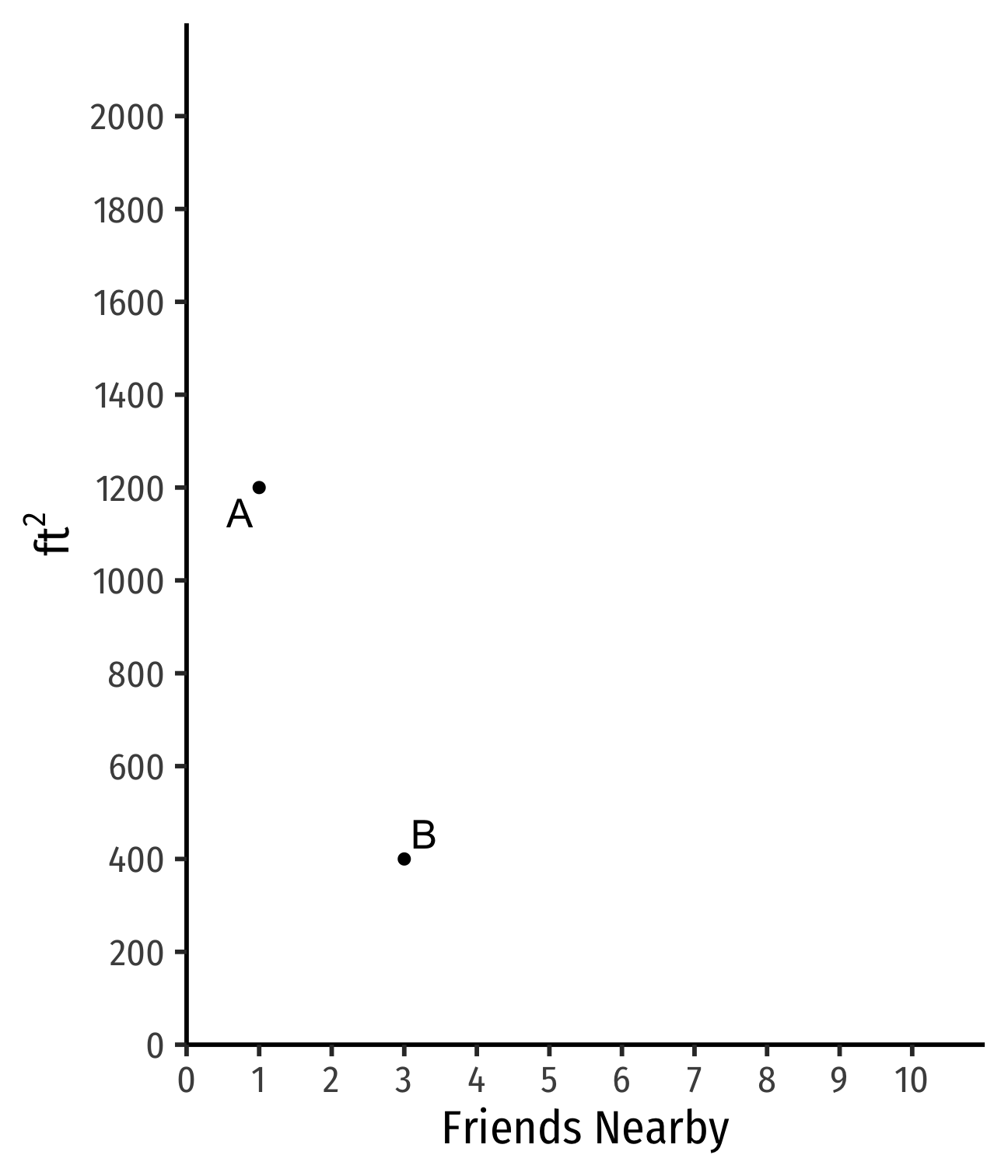
Example:
Apt. A has 1 friend nearby and is 1,200 ft2
B has more friends but less ft2
Indifference Curves: Example
Example:
Apt. A has 1 friend nearby and is 1,200 ft2
B has more friends but less ft2
C has still more friends but less ft2
Indifference Curves: Example
Example:
Apt. A has 1 friend nearby and is 1,200 ft2
B has more friends but less ft2
C has still more friends but less ft2
A∼B∼C: on same indifference curve
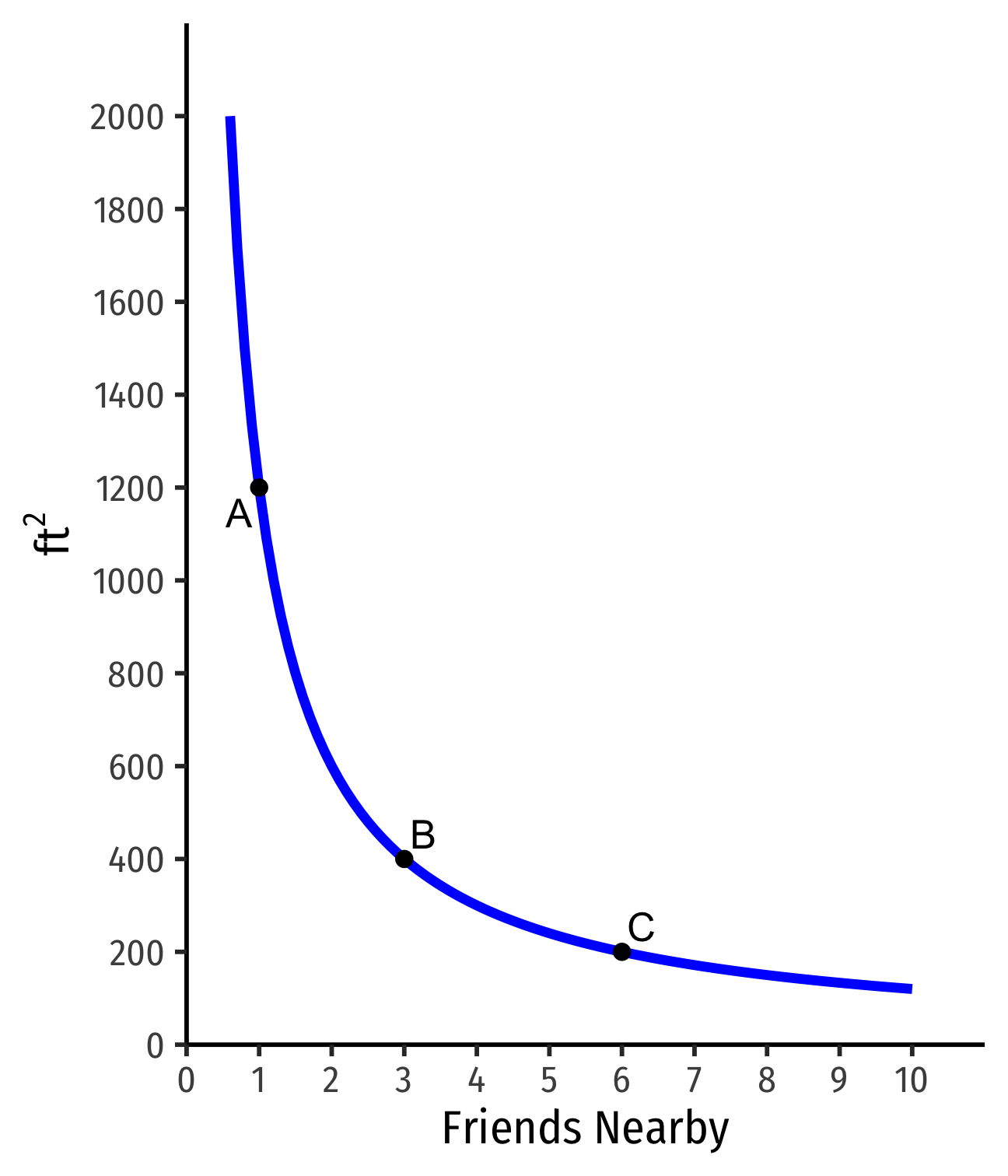
Indifference Curves: Example
- Indifferent between all apartments on the same curve
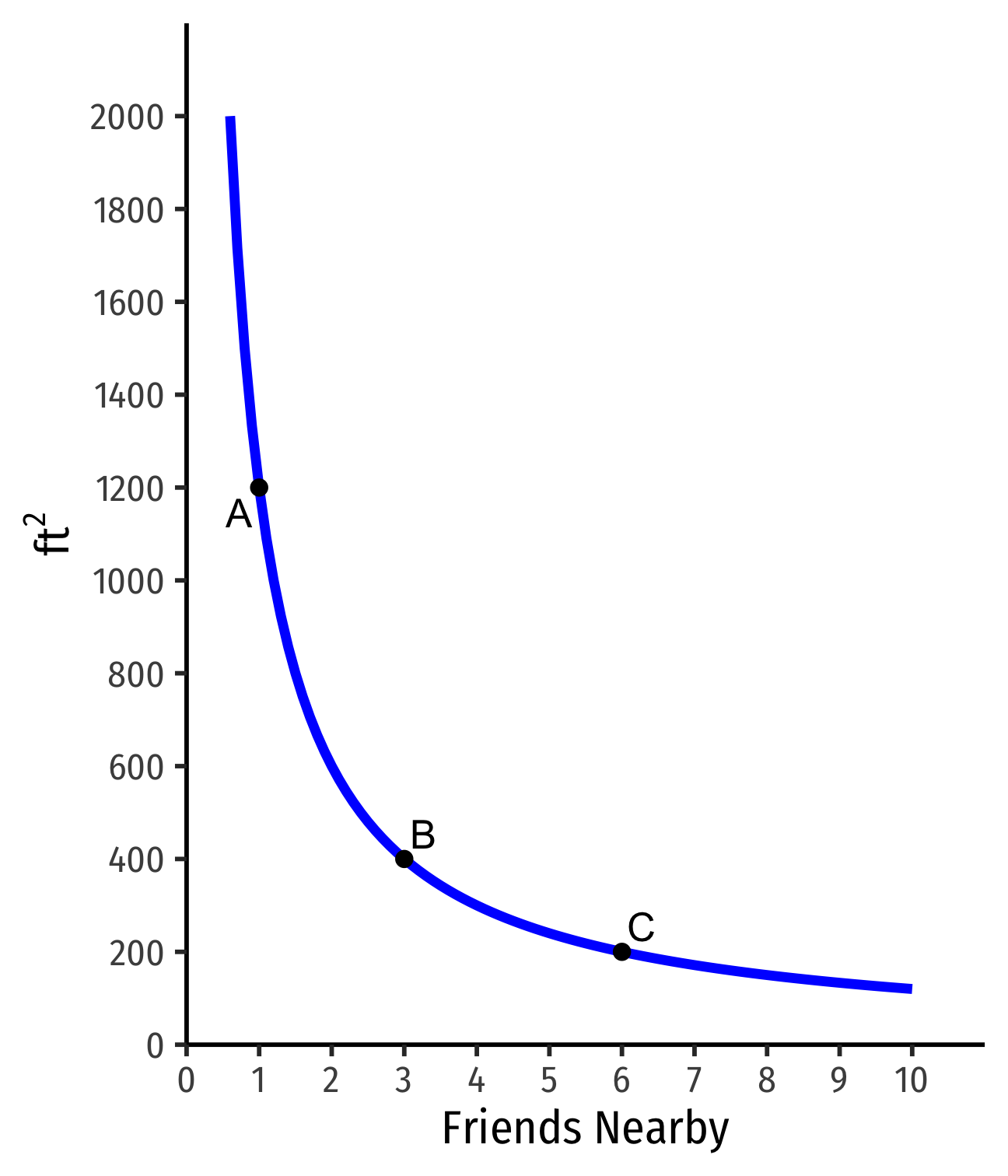
Indifference Curves: Example
Indifferent between all apartments on the same curve
Apts above curve are preferred over apts on curve
- D≻A∼B∼C
- On a higher curve
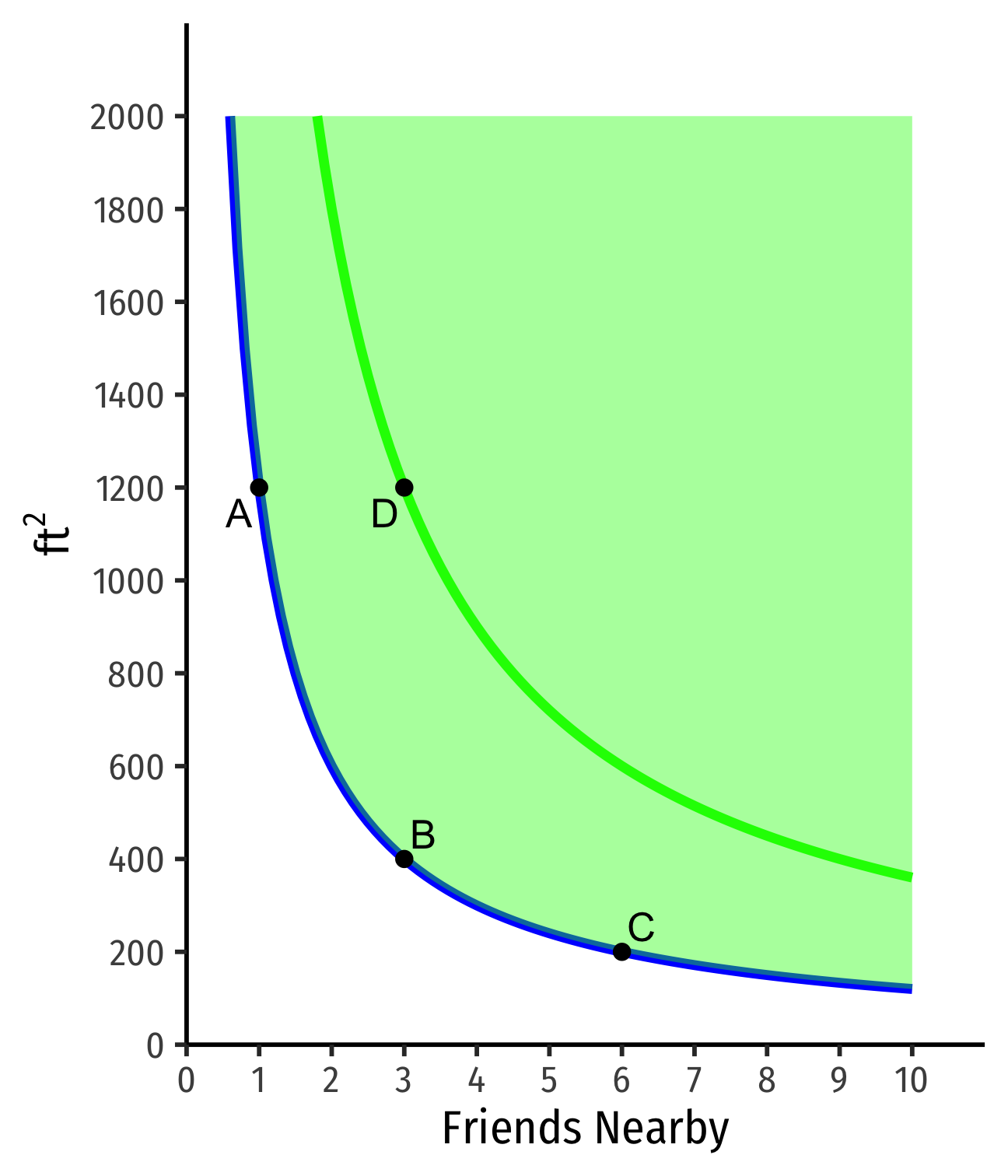
Indifference Curves: Example
Indifferent between all apartments on the same curve
Apts above curve are preferred over apts on curve
- D≻A∼B∼C
- On a higher curve
- Apts below curve are less preferred than apts on curve
- E≺A∼B∼C
- On a lower curve
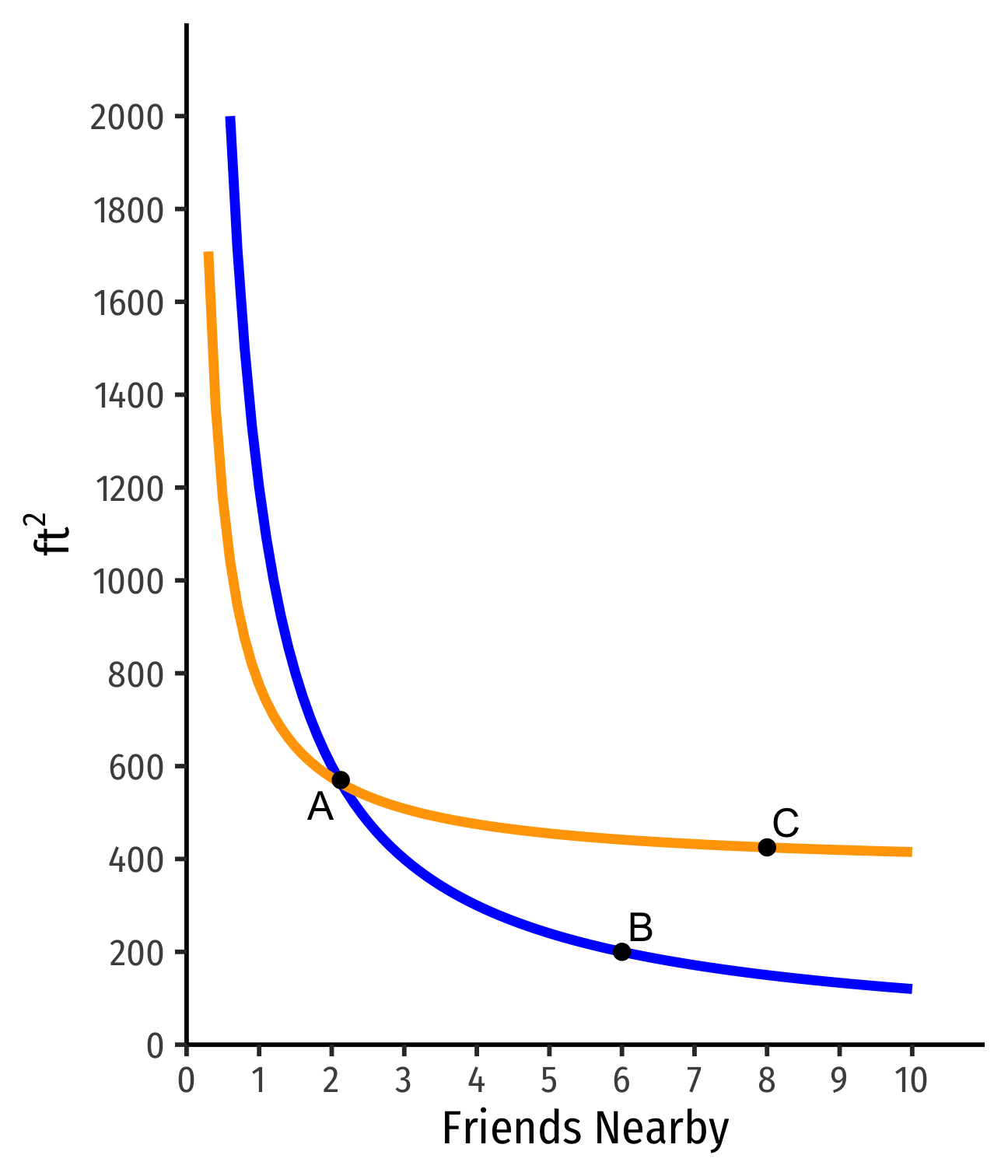
Curves Never Cross!
- Indifference curves can never cross: preferences are transitive
- If I prefer A≻B, and B≻C, I must prefer A≻C
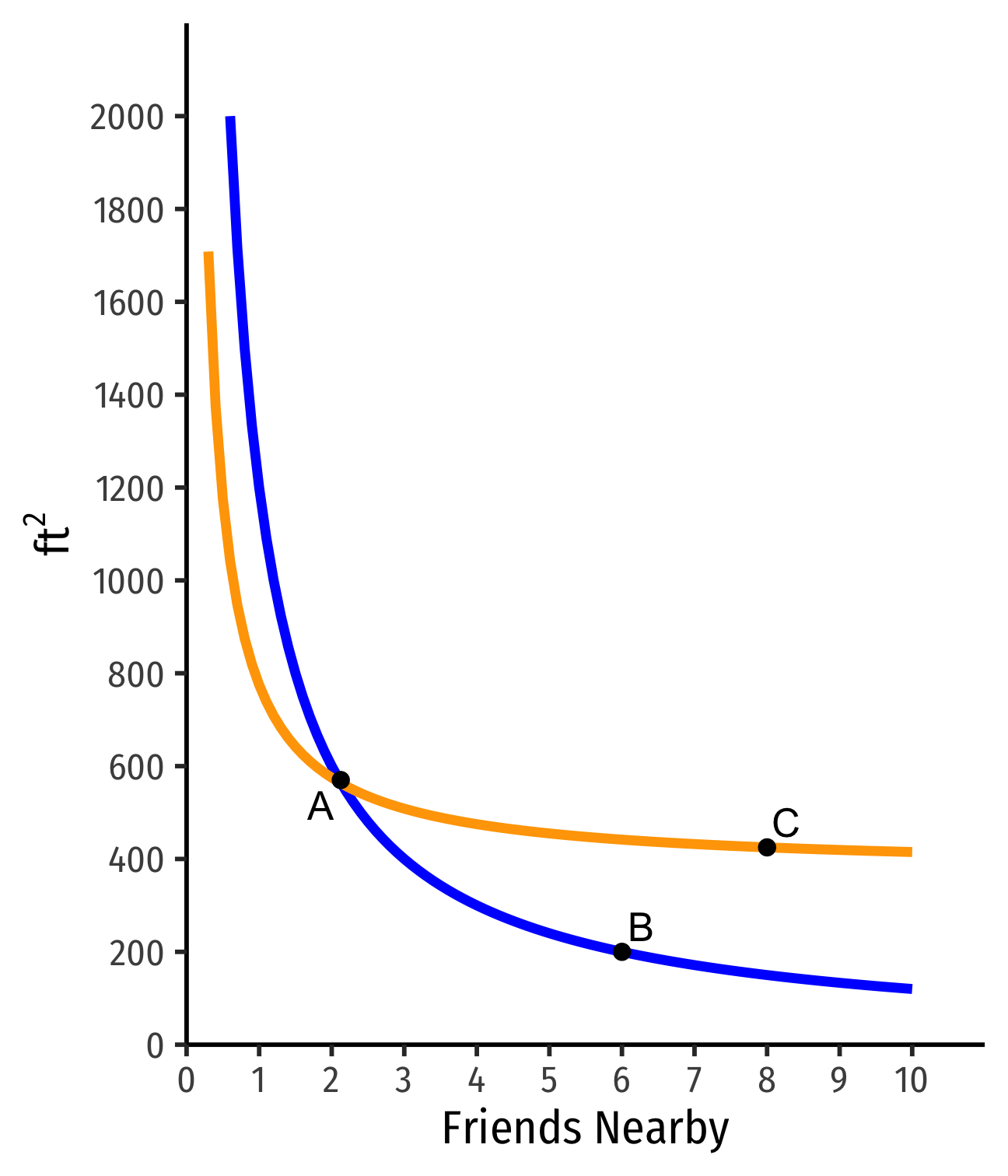
Curves Never Cross!
Indifference curves can never cross: preferences are transitive
- If I prefer A≻B, and B≻C, I must prefer A≻C
Suppose two curves crossed:
- A∼B
- B∼C
- But C ≻ B!
- Doesn't make sense (not transitive)!
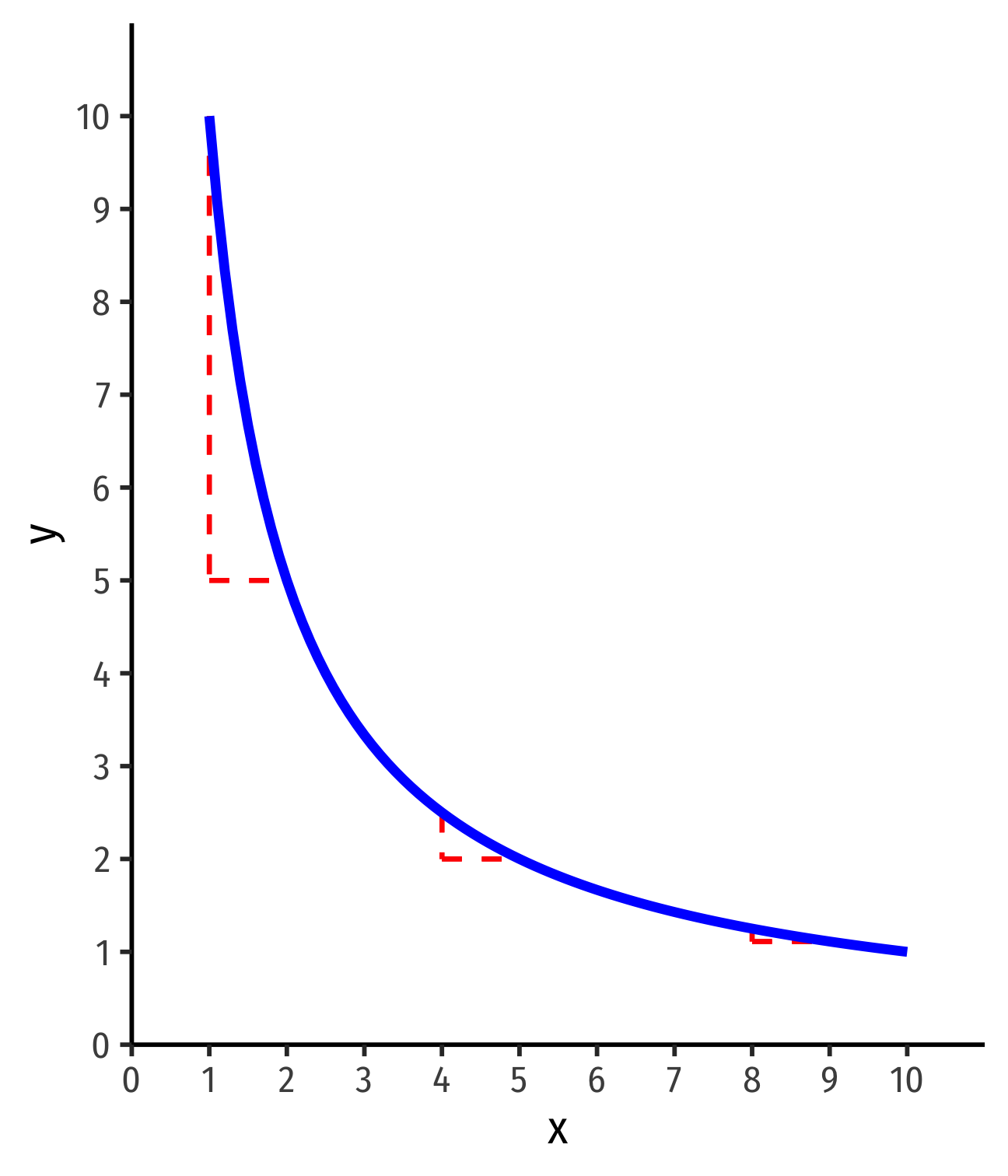
Marginal Rate of Substitution
Marginal Rate of Substitution I
- If I find another apt with 1 fewer friend nearby, how many more ft2 would you need to keep you satisfied?

Marginal Rate of Substitution I
If I find another apt with 1 fewer friend nearby, how many more ft2 would you need to keep you satisfied?
Marginal Rate of Substitution (MRS): rate at which you trade away one good for more of the other and remain indifferent
Think of this as the relative value you place on good x:
“I am willing to give up (MRS) units of y to consume 1 more unit of x and stay satisfied.”

Marginal Rate of Substitution II

Marginal Rate of Substitution II
- MRS = slope of the indifference curve
MRSx,y=−ΔyΔx=riserun
Amount of y given up for 1 more x
Note: slope (MRS) changes along the curve!
MRS vs. Budget Constraint Slope
Budget constraint (slope) from before measured the market’s tradeoff between x and y based on market prices
MRS here measures your personal evaluation of x vs. y based on your preferences
Foreshadowing: what if these two rates are different? Are you truly optimizing?

Utility
So Where are the Numbers?
Long ago (1890s), utility considered a real, measurable, cardinal scale†
Utility thought to be lurking in people's brains
- Could be understood from first principles: calories, water, warmth, etc
Obvious problems

† “Neuroeconomics” & cognitive scientists are re-attempting a scientific approach to measure utility
Utility Functions?
More plausibly infer people's preferences from their actions!
- “Actions speak louder than words”
Principle of Revealed Preference: if a person chooses x over y, and both are affordable, then they must prefer x⪰y
Flawless? Of course not. But extremely useful approximation!
- People tend not to leave money on the table

Utility Functions!
A utility function u(⋅)† represents preference relations (≻,≺,∼)
Assign utility numbers to bundles, such that, for any bundles a and b: a≻b⟺u(a)>u(b)

† The ⋅ is a placeholder for whatever goods we are considering (e.g. x, y, burritos, lattes, etc)
Utility Functions, Pural I
Example: Imagine three alternative bundles of (x,y): a=(1,2)b=(2,2)c=(4,3)
Utility Functions, Pural I
Example: Imagine three alternative bundles of (x,y): a=(1,2)b=(2,2)c=(4,3)
- Let u(⋅) assign each bundle a utility of:
| u(⋅) |
|---|
| u(a)=1 |
| u(b)=2 |
| u(c)=3 |
Utility Functions, Pural I
Example: Imagine three alternative bundles of (x,y): a=(1,2)b=(2,2)c=(4,3)
- Let u(⋅) assign each bundle a utility of:
| u(⋅) |
|---|
| u(a)=1 |
| u(b)=2 |
| u(c)=3 |
- Does this mean that bundle c is 3 times the utility of a?
Utility Functions, Pural II
Example: Imagine three alternative bundles of (x,y): a=(1,2)b=(2,2)c=(4,3)
- Now consider a 2nd function v(⋅):
| u(⋅) | v(⋅) |
|---|---|
| u(a)=1 | v(a)=3 |
| u(b)=2 | v(b)=5 |
| u(c)=3 | v(c)=7 |
Utility Functions, Pural III
Utility numbers have an ordinal meaning only, not cardinal
Both are valid utility functions:†
- u(c)>u(b)>u(a) ✅
- v(c)>v(b)>v(a) ✅
- because c≻b≻a
Only the ranking of utility numbers matters!

† See the Mathematical Appendix in Today's Class Page for why.
Utility Functions and Indifference Curves I
Two tools to represent preferences: indifference curves and utility functions
Indifference curve: all equally preferred bundles ⟺ same utility level
Each indifference curve represents one level (or contour) of utility surface (function)

Marginal Utility
MRS and Marginal Utility I
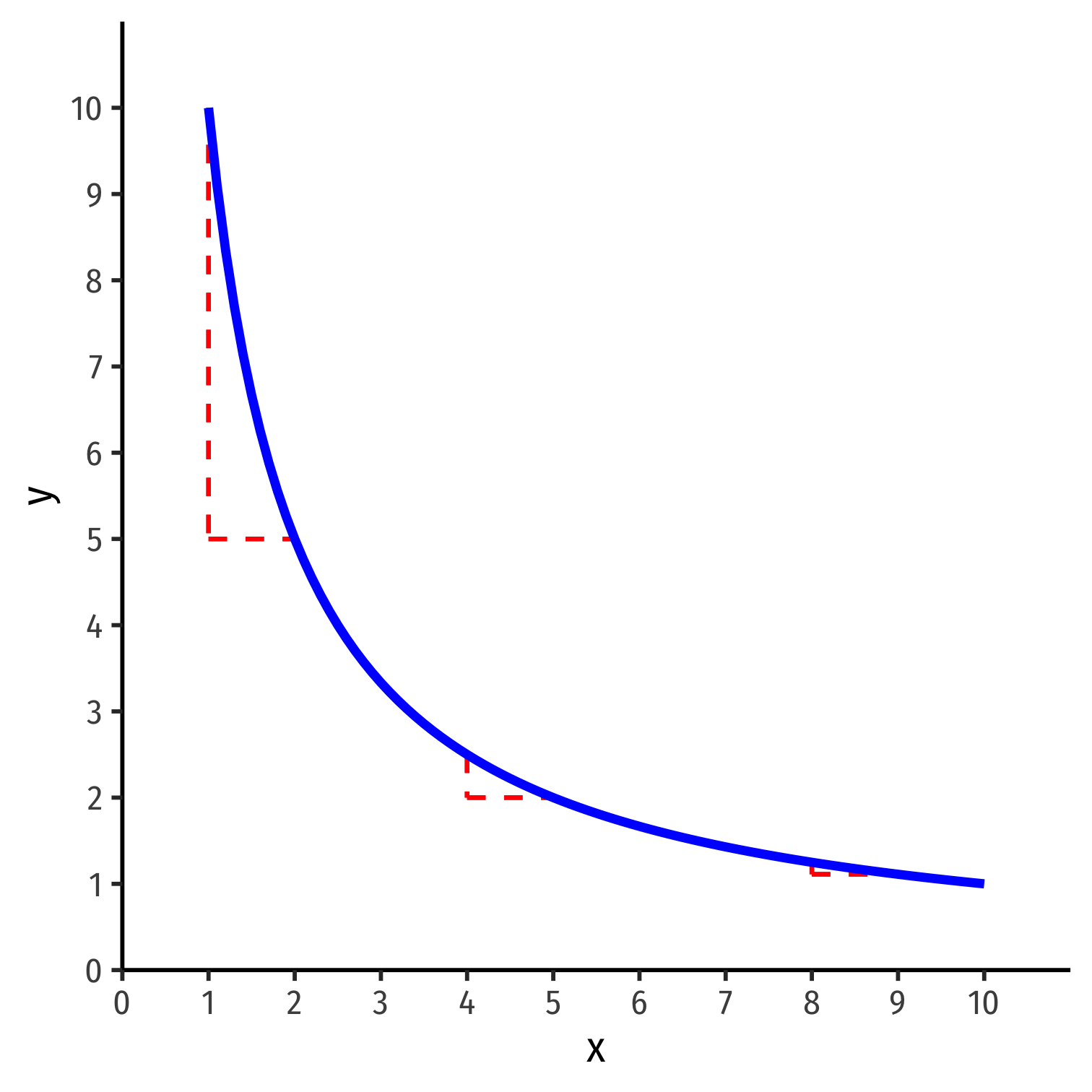
Recall: marginal rate of substitution MRSx,y is slope of the indifference curve
- Amount of y given up for 1 more x
How to calculate MRS?
- Recall it changes (not a straight line)!
- We can calculate it using something from the utility function
MRS and Marginal Utility II
- Marginal utility: change in utility from a marginal increase in consumption
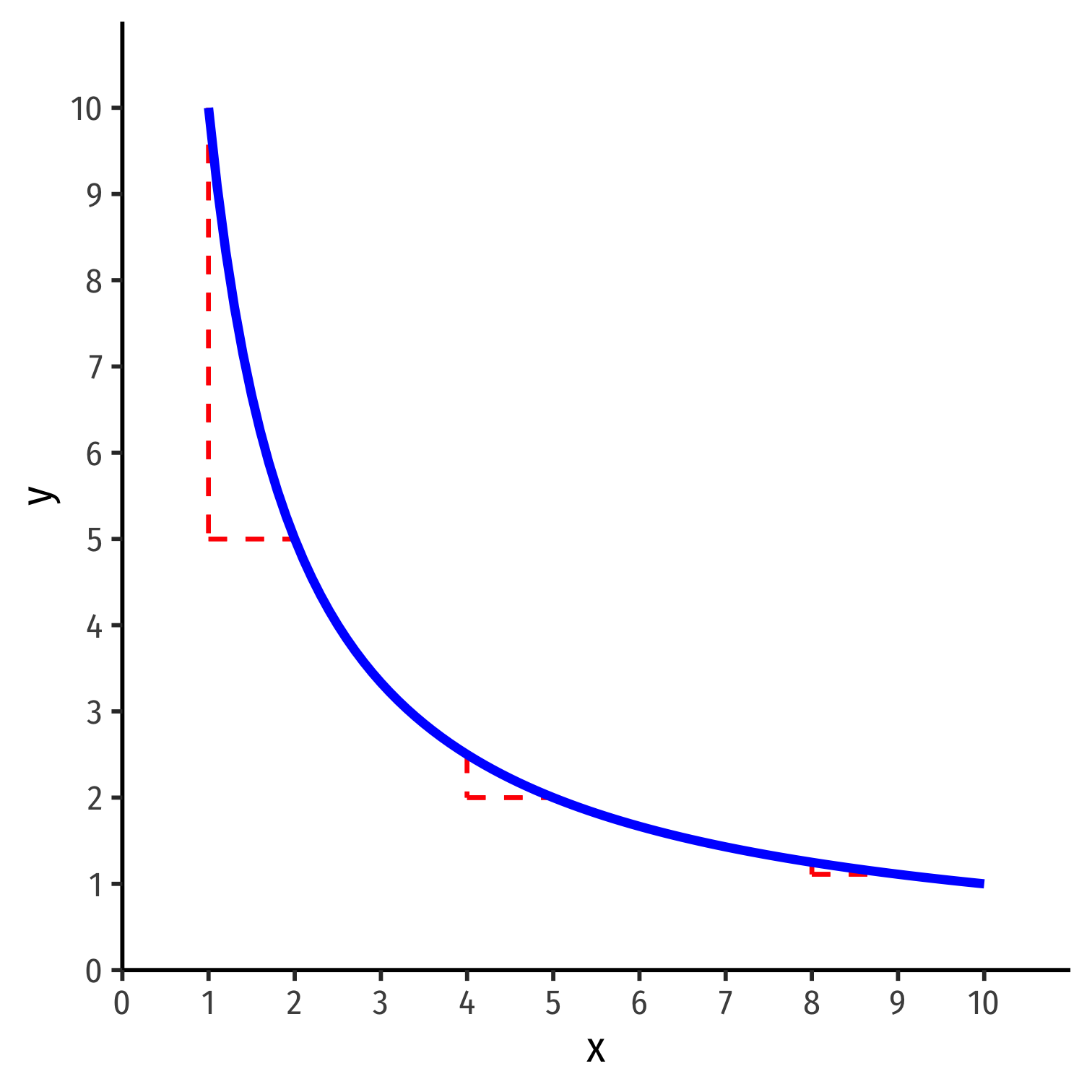
MRS and Marginal Utility II
- Marginal utility: change in utility from a marginal increase in consumption
Marginal utility of x: MUx=Δu(x,y)Δx
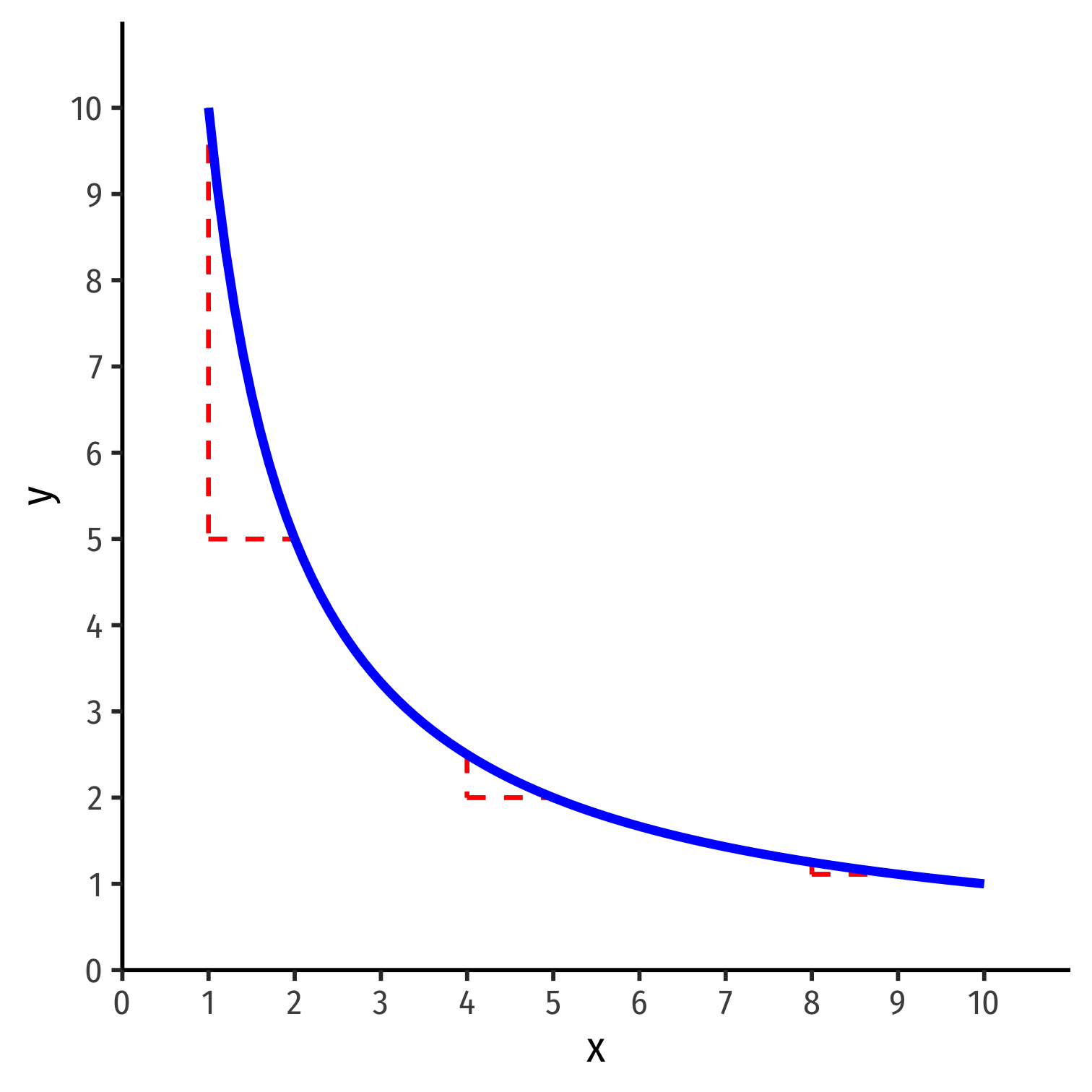
MRS and Marginal Utility II
- Marginal utility: change in utility from a marginal increase in consumption
Marginal utility of x: MUx=Δu(x,y)Δx
Marginal utility of y: MUy=Δu(x,y)Δy
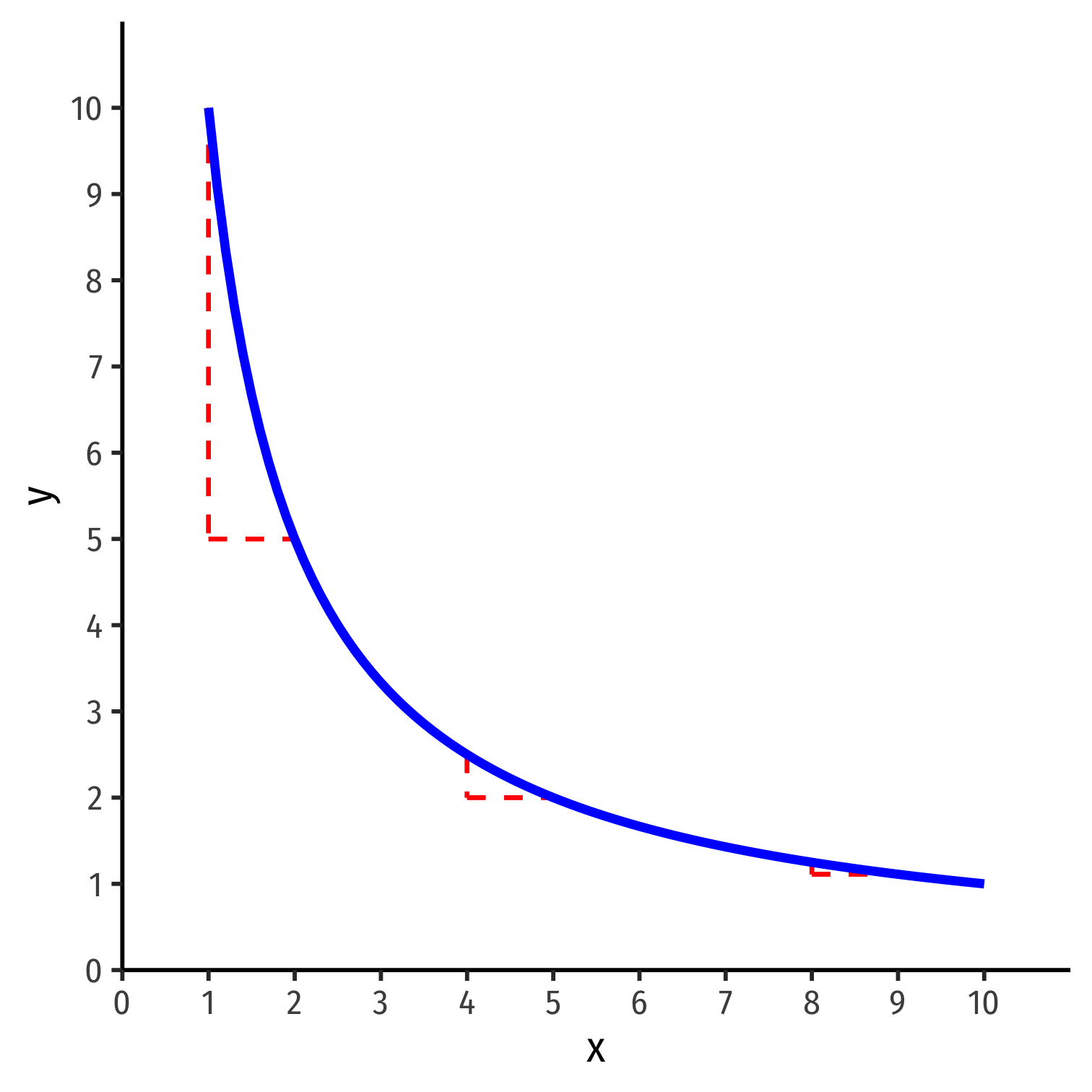
MRS and Marginal Utility II
- Marginal utility: change in utility from a marginal increase in consumption
- Math (calculus): “marginal” ⟺ “derivative with respect to”
MUx=∂u(x,y)∂x
- I will always derive marginal utility functions for you
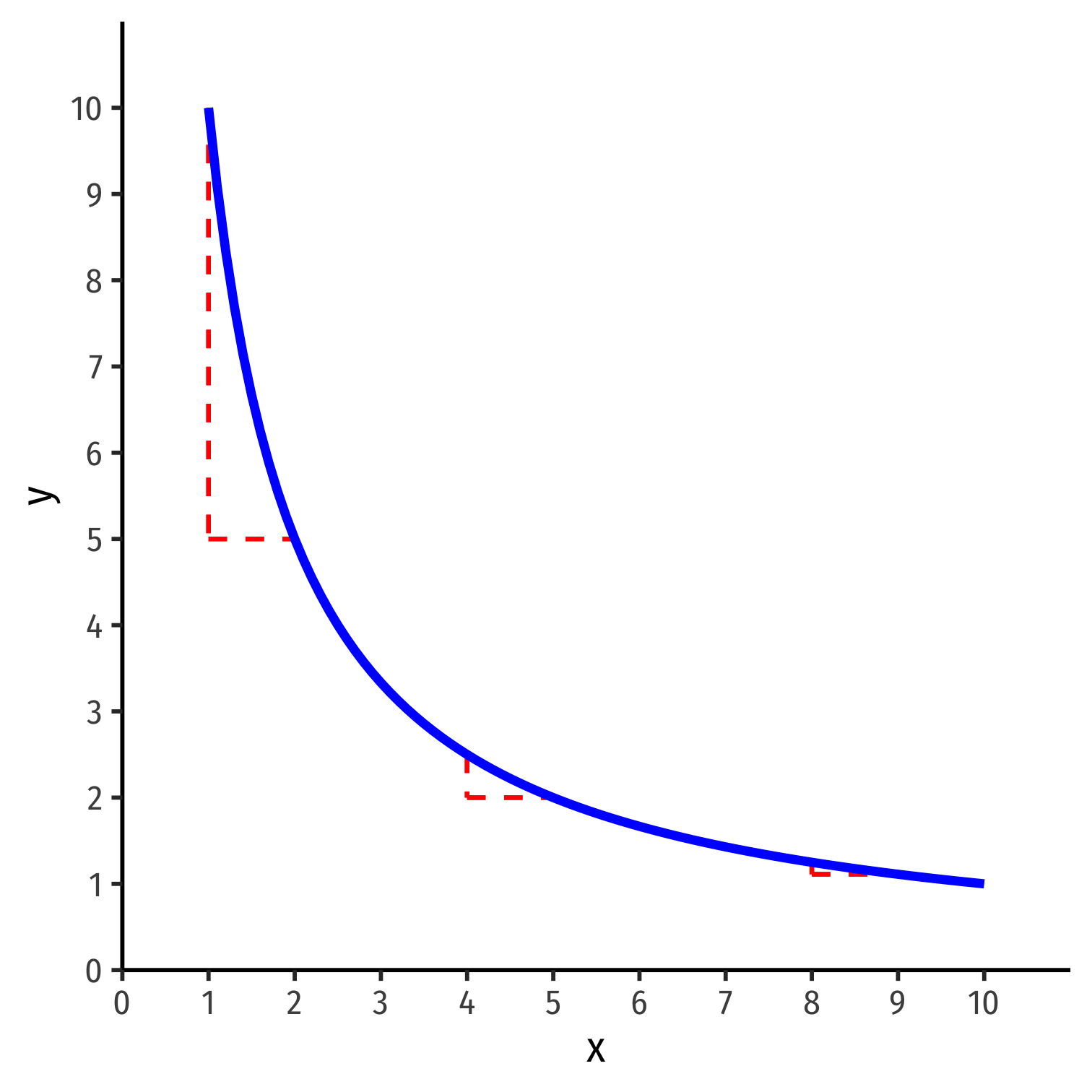
MRS and Marginal Utility: Example
Example: For an example utility function:
u(x,y)=x2+y3
- Marginal utility of x: MUx=2x
- Marginal utility of y: MUy=3y2
- Again, I will always derive marginal utility functions for you
MRS Equation and Marginal Utility
- Relationship between MU and MRS:
ΔyΔxMRS=−MUxMUy
- See proof in today's class notes
“I am willing to give up MUxMUy units of y to consume 1 more unit of x and stay satisfied.”
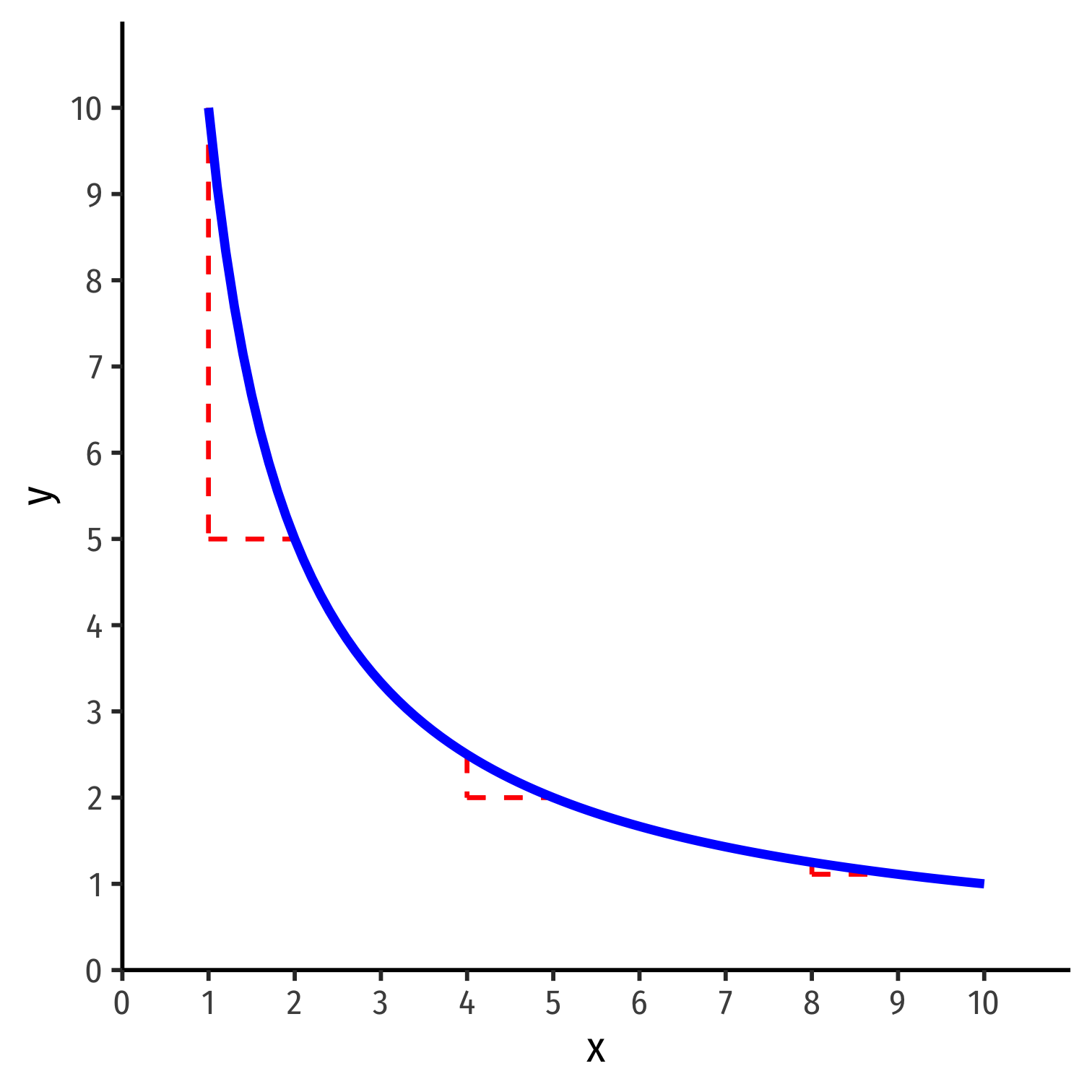
Important Insights About Value
“I am willing to give up MUxMUy units of y to consume 1 more unit of x and stay satisfied.”
- We can't measure MU's, but we can measure MRSx,y and infer the ratio of MU's!
- Example: if MRSx,y=5, a unit of good x gives 5 times the marginal utility of good y at the margin
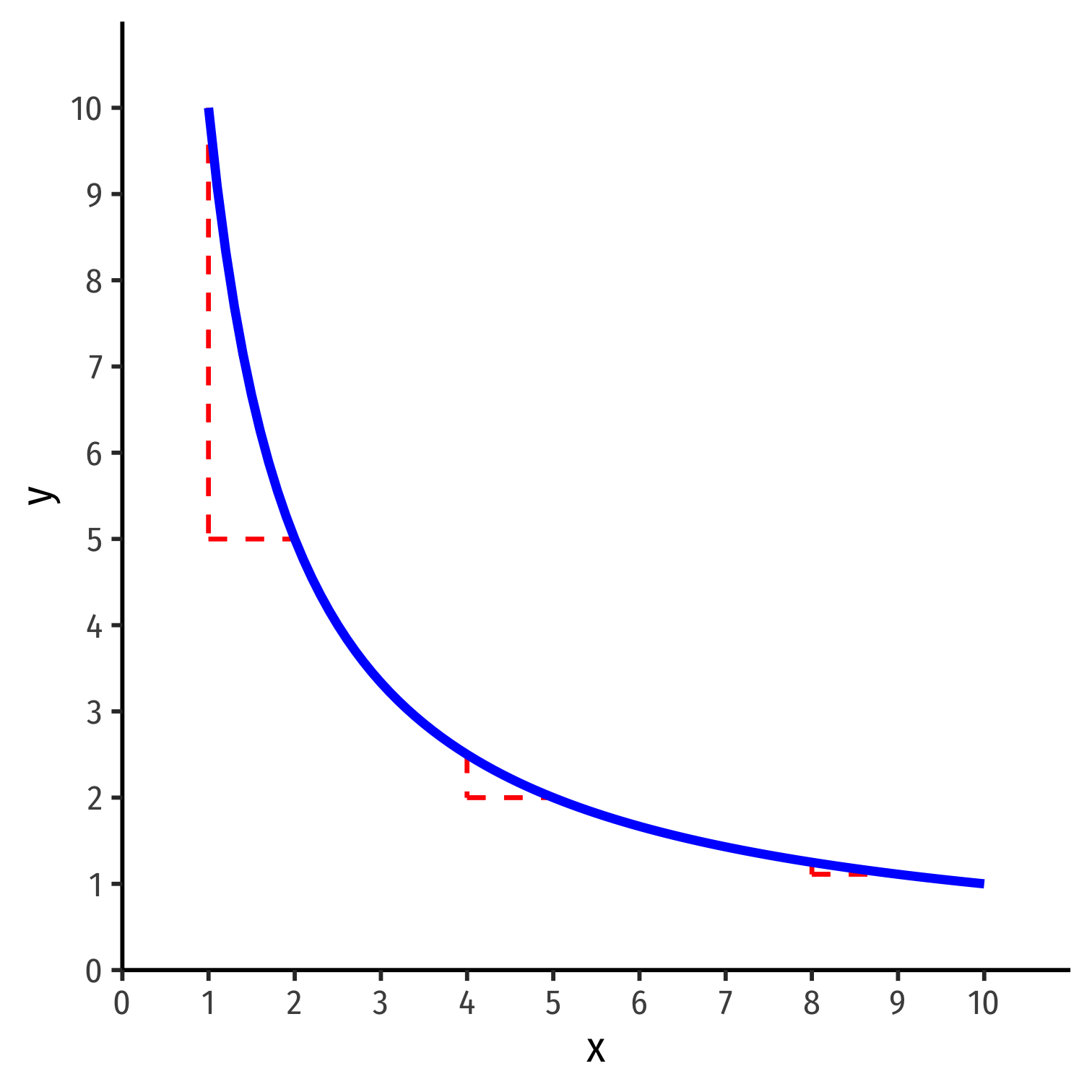
Important Insights About Value
Value is subjective
- Each of us has our own preferences that determine our ends or objectives
- Choice is forward looking: a comparison of your expectations about opportunities
Preferences are not comparable across individuals
- Only individuals know what they give up at the moment of choice

Important Insights About Value
- Value inherently comes from the fact that we must make tradeoffs
- Making one choice means having to give up pursuing others!
- The choice we pursue at the moment must be worth the sacrifice of others! (i.e. highest marginal utility)

Diminishing Marginal Utility
The Law of Diminishing Marginal Utility: each marginal unit of a good consumed tends to provide less marginal utility than the previous unit, all else equal
- As you consume more x:
- ↓MUx
- ↓MRSx,y: willing to give up fewer units of y for x

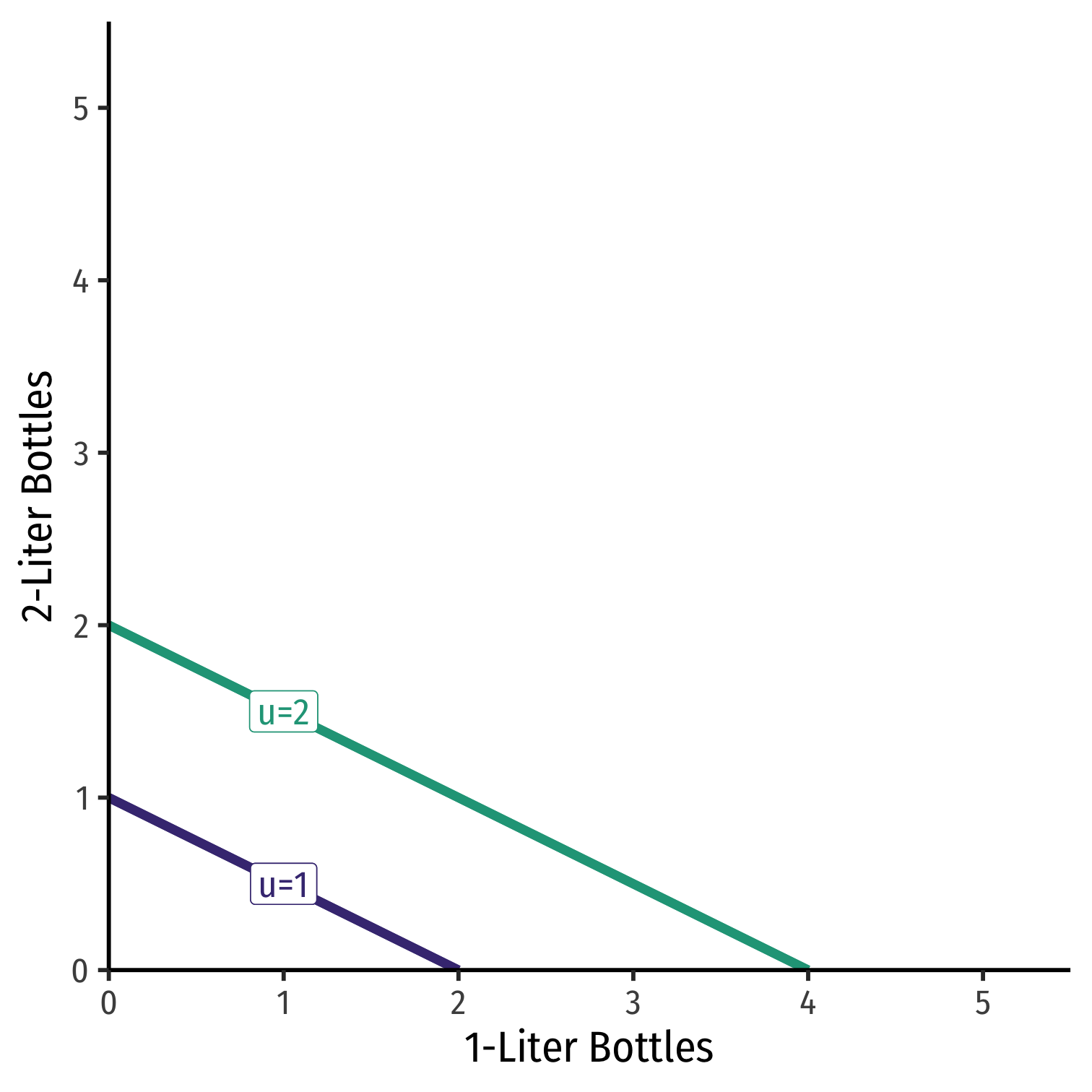
Special Case: Substitutes
Example: Consider 1-Liter bottles of coke and 2-Liter bottles of coke
Always willing to substitute between Two 1-L bottles for One 2-L bottle
Perfect substitutes: goods that can be substituted at same fixed rate and yield same utility
MRS1L,2L=−0.5 (a constant!)
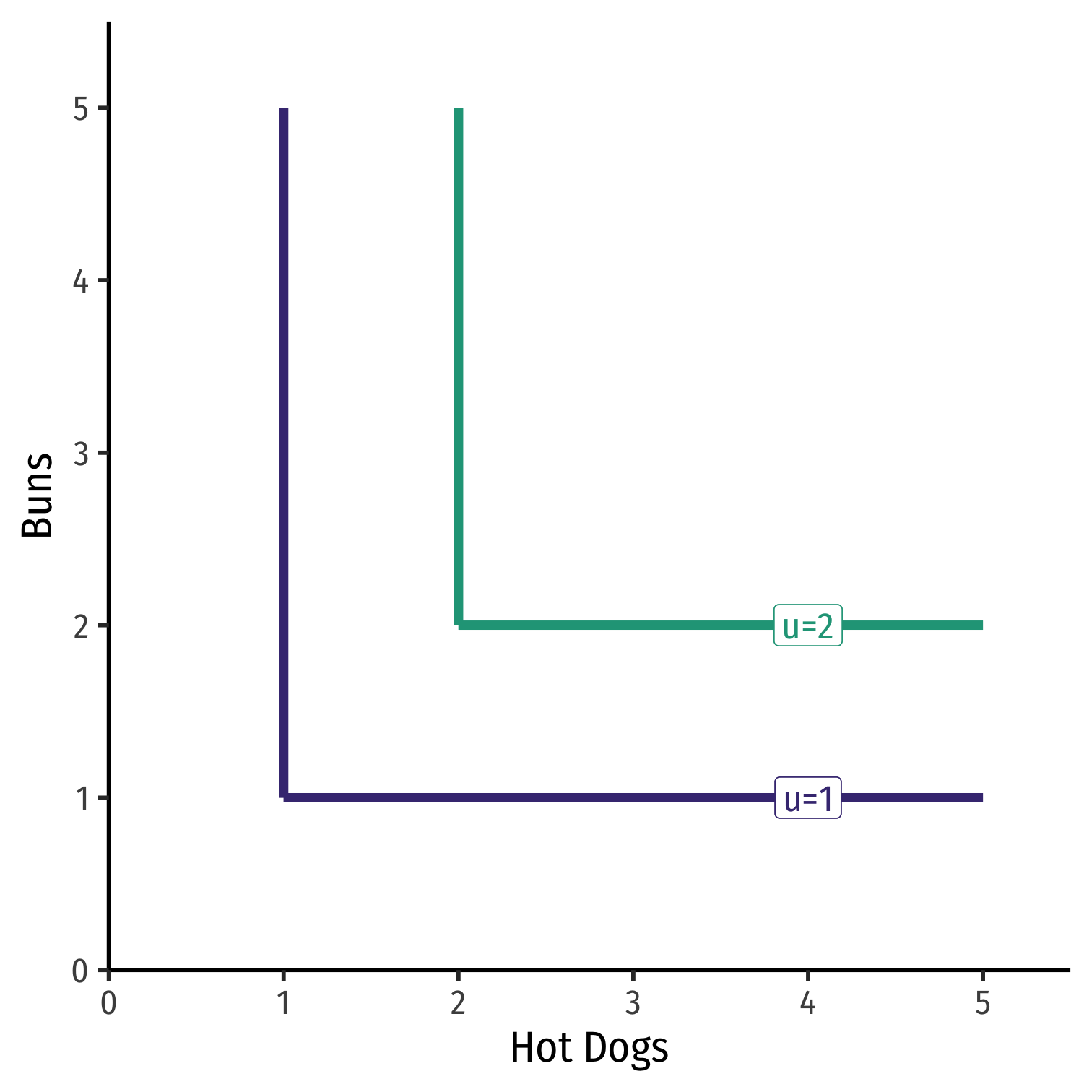
Special Case: Complements
Example: Consider hot dogs and hot dog buns
Always consume together in fixed proportions (in this case, 1 for 1)
Perfect complements: goods that can be consumed together in same fixed proportion and yield same utility
MRSH,B= ?
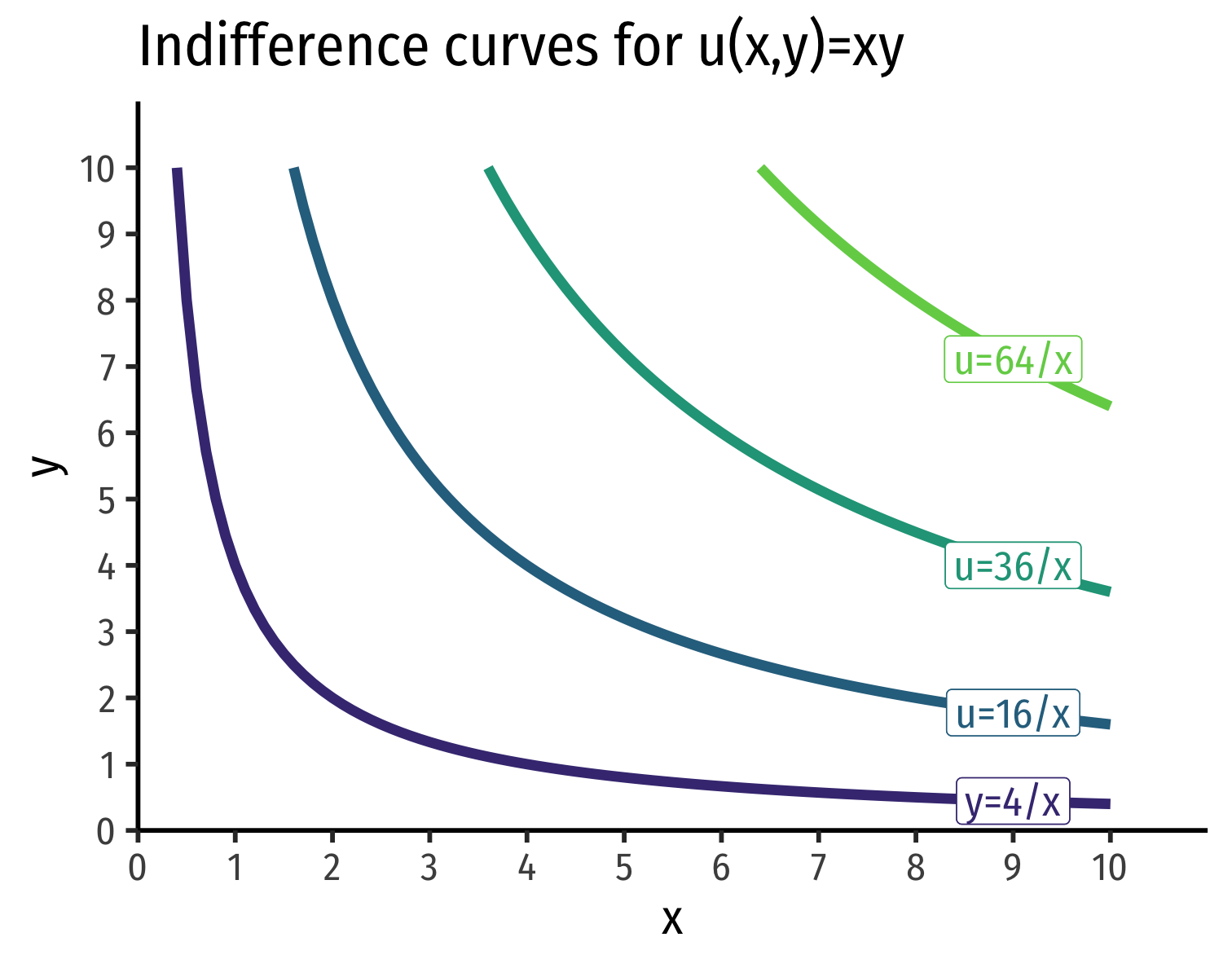
Cobb-Douglas Utility Functions
- A very common functional form in economics is Cobb-Douglas
u(x,y)=xayb
- Extremely useful, you will see it often!
- Lots of nice, useful properties (we'll see later)
- See the appendix in today's class page
Practice
Example: Suppose you can consume apples (a) and broccoli (b), and earn utility according to:
u(a,b)=2abMUa=2bMUb=2a
Put a on the horizontal axis and b on the vertical axis. Write an equation for MRSa,b.
Would you prefer a bundle of (1,4) or (2,2)?
Suppose you are currently consuming 1 apple and 4 broccoli. a. How many units of broccoli are you willing to give up to eat 1 more apple and remain indifferent? b. How much more utility would you get if you were to eat 1 more apple?
Repeat question 3, but for when you are consuming 2 of each good.