Problem Set 4
Please read the instructions for completing homeworks.
Answers
Concepts and Critical Thinking
Please answer the following questions briefly (1-3 sentences). Use examples as necessary. Be sure to label graphs fully, if appropriate.
Question 1
What is the difference between accounting profit and economic profit? Is it possible for a firm to be profitable in an accounting sense but not an economic sense? Is it possible for a firm to be profitable in an economic sense but not an accounting sense?
Question 2
In a competitive industry, with identical firms (e.g. all firms have the same costs), why are profits normal (zero) in the long run?
Question 3
In a competitive industry, even among firms with significant cost differences (e.g. there are economic rents), why do profits tend to return to normal (0) in the long run?
Question 4
For each of the following pairs of goods, which do you expect to be more elastically supplied, and why?
- Toothpicks vs. Scotch whisky
- Construction workers in Frederick, MD vs. construction workers in the State of Maryland
- Supply of breakfast cereal vs. supply of food
- Original Van Gogh paintings vs. reproductions of Van Gogh paintings
- Gasolone tomorrow vs. gasoline over the next 10 years
Problems
Show all work for calculations. You may lose points, even if correct, for missing work. Be sure to label graphs fully, if appropriate.
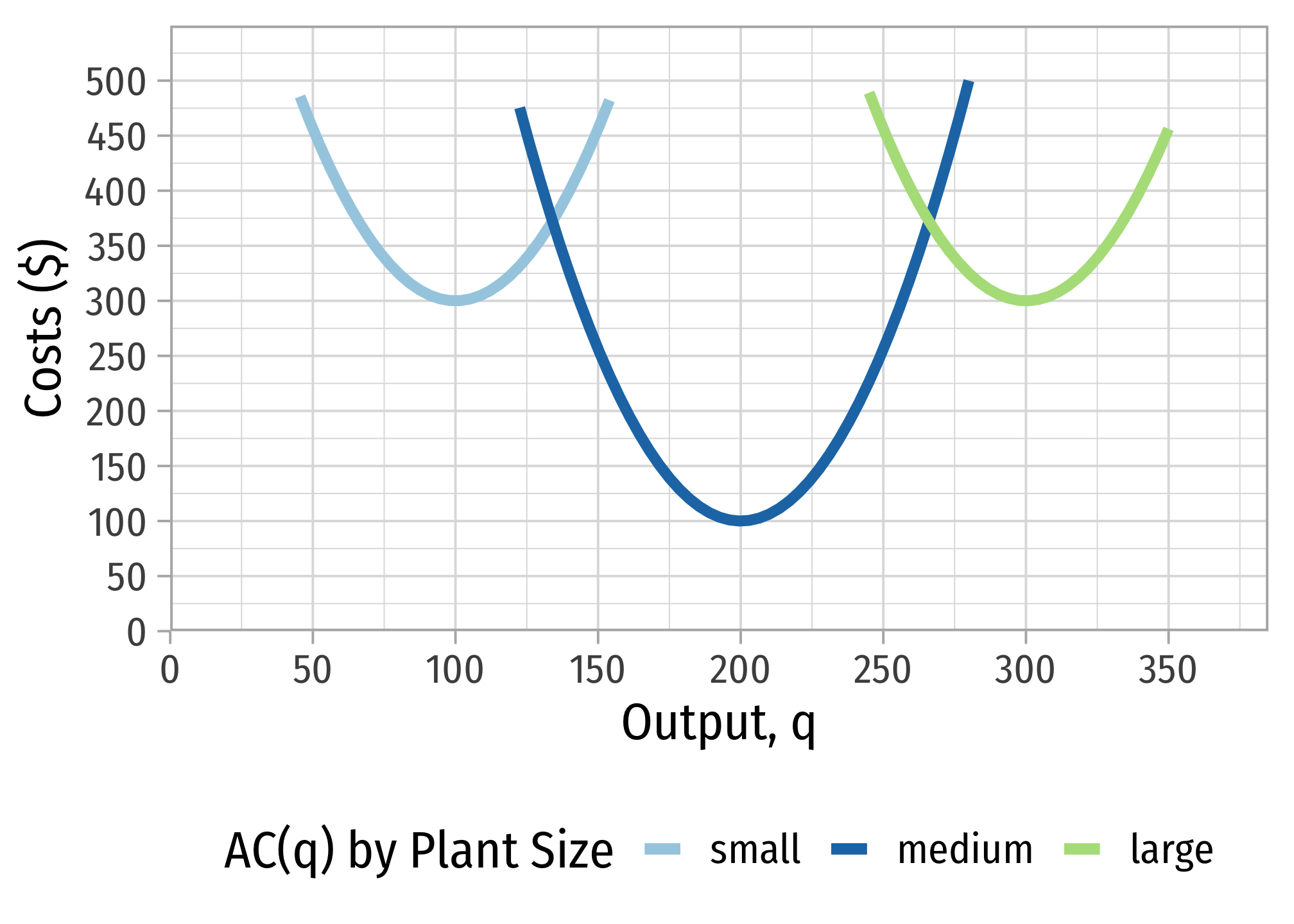
Question 5
Mike’s Bikes produces racing bicycles. Consider the following graph, which illustrates the short run average total cost curves corresponding to three possible plant sizes Mike could produce with: a small plant, a medium plant, and a large plant.
Part A
If Mike wanted to produce 125 bikes, what size plant should be used, and why? What about 150 bikes?
Part B
If Mike wanted to produce 250 bikes, what size plant should be used, and why? What about 275 bikes?
Part C
Draw the long run average cost curve on the graph provided (or sketch one yourself).
Part D
Suppose Mike’s long run total cost function can be roughly expressed as:
with a long run marginal cost function of Find the quantity of bikes where long run average cost is minimized. Plot this point on your graph. At what range of production does Mike experience economies of scale? At what range of production does Mike experience diseconomies of scale?
Question 6
Daniel’s Midland Archers has the following cost structure for producing archery bows:
Part A
Write an equation for fixed costs,
Part B
Write an equation for variable costs,
Part C
Write an equation for average fixed costs,
Part D
Write an equation for average variable costs,
Part E
Write an equation for average (total) costs,
Part F
At what price does Daniel’s Midland Archers break even?
Part G
Below what price would Daniel’s Midland Archers shut down in the short-run?
Part H
Write an equation for the firm’s short-run supply curve, and sketch a rough graph.
Part I
What differences would there be between Daniel’s Midland Archers supply curve in the short run versus the long run?
Part J
In the long run, with many identical sellers of archery bows, what would we expect to be the equilibrium price in the market?
Question 7
The supply of movie tickets in a small town is given by:
Part A
Write the inverse supply function.
Part B
Calculate the price elasticity of supply at a price of $6 per ticket.
Part C
Calculate the price elasticity of supply at a price of $8 per ticket.